No CrossRef data available.
Article contents
Strong Converse Inequalities for Averages in Weighted Lp Spaces on [-1,1]
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Averages in weighted spaces
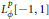$L_{\phi }^{p}[-1,1]$
defined by additions on 
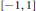$[-1,\,1]$ will be shown to satisfy strong converse inequalities of type 
$\text{A}$ and 
$\text{B}$ with appropriate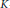 
$K$-functionals. Results for higher levels of smoothness are achieved by combinations of averages. This yields, in particular, strong converse inequalities of type 
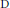$\text{D}$ between 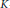$K$-functionals and suitable difference operators.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1999
References
[Di-Fe]
Ditzian, Z. andFelten, M., Averages using translation induced by Laguerre and Jacobi expansions. Constr. Approx., to appear.Google Scholar
[Di-Iv]
Ditzian, Z. and Ivanov, K., Strong converse inequalities. J. Anal. Math.. 61 (1993), 61–111.Google Scholar
[Di-Ru]
Ditzian, Z. and Runovskii, K., Averages and K-functionals related to the Laplacian. J. Approx. Theory, to appear.Google Scholar
[Fe1]
Felten, M., A Smoothness Concept forWeighted Lp Spaces on[−1; 1]
Acta Sci.Math.. 62 (1996), 217–230.Google Scholar
[Fe2]
Felten, M., A modulus of smoothness based on an algebraic addition. Aequationes Math.. 54 (1997), 56–73.Google Scholar
[Fe3]
Felten, M., Characterization of best algebraic approximation by an algebraic modulus of smoothness. J. Approx. Theory. 89 (1997), 1–25.Google Scholar
You have
Access