Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Holland, W. Charles
1983.
Universal Algebra and Lattice Theory.
Vol. 1004,
Issue. ,
p.
153.
Holland, W. Charles
1984.
Orders: Description and Roles - In Set Theory, Lattices, Ordered Groups, Topology, Theory of Models and Relations, Combinatorics, Effectiveness, Social Sciences, Proceedings of the Conference on Ordered Sets and their Application Château dc la Tourcttc; Ordres: Description et Rôles - En Théorie des Treillis, des Groupes Ordonnés; en Topologie, Théorie des Modèles et des Relations, Cornbinatoire, Effectivité, Sciences Sociales, Actes de la Conférence sur ies Ensembles Ordonnés et leur Applications Château de la Tourette.
Vol. 99,
Issue. ,
p.
151.
Huss, M.E
and
Reilly, N.R
1984.
On reversing the order of a lattice ordered group.
Journal of Algebra,
Vol. 91,
Issue. 1,
p.
176.
Arora, Ashok Kumar
1985.
Quasi-varieties of lattice ordered groups.
Algebra Universalis,
Vol. 20,
Issue. 1,
p.
34.
Holland, W. Charles
and
Reilly, Norman R.
1987.
Metabelian varieties ofl-groups which contain no non-abeliano-groups.
Algebra Universalis,
Vol. 24,
Issue. 3,
p.
204.
Powell, Wayne B.
1989.
Ordered Algebraic Structures.
p.
11.
Hansen, Mary E.
1991.
The lex property of varieties of lattice ordered groups.
Algebra Universalis,
Vol. 28,
Issue. 4,
p.
535.
Darnel, Michael R.
1993.
Varieties minimal over representable varieties of lattice-ordered groups.
Communications in Algebra,
Vol. 21,
Issue. 8,
p.
2637.
Darnel, Michael R.
1993.
Ordered Algebraic Structures.
p.
31.
Kopytov, V. M.
and
Medvedev, N. Ya.
1996.
Ordered Groups and Infinite Permutation Groups.
p.
1.
 determines a variety of groups, namely the variety of groups generated by the groups i n
determines a variety of groups, namely the variety of groups generated by the groups i n 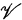 . In this paper a completely new and different correspondence between varieties of groups and varieties of lattice ordered groups is developed. It is known that the variety of representable lattice ordered groups is defined by the law z+ Λ u-1z-u = 1. Here we consider the varieties defined by laws of this form where u is restricted to lie in some fully invariant subgroup of the free group Fx on a countable set X. All the varieties considered contain the variety of representable l-groups and therefore the free group with appropriate ordering.
. In this paper a completely new and different correspondence between varieties of groups and varieties of lattice ordered groups is developed. It is known that the variety of representable lattice ordered groups is defined by the law z+ Λ u-1z-u = 1. Here we consider the varieties defined by laws of this form where u is restricted to lie in some fully invariant subgroup of the free group Fx on a countable set X. All the varieties considered contain the variety of representable l-groups and therefore the free group with appropriate ordering.