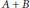Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tian, Yongge
2010.
Equalities and inequalities for inertias of hermitian matrices with applications.
Linear Algebra and its Applications,
Vol. 433,
Issue. 1,
p.
263.
Tian, Yongge
2011.
Maximization and minimization of the rank and inertia of the Hermitian matrix expression A-BX-(BX)* with applications.
Linear Algebra and its Applications,
Vol. 434,
Issue. 10,
p.
2109.
Tian, Yongge
2015.
A survey on rank and inertia optimization problems of the matrix-valued
function $A + BXB^{*}$.
Numerical Algebra, Control & Optimization,
Vol. 5,
Issue. 3,
p.
289.
Wu, Sheng-Jhih
and
Chu, Moody T
2017.
Solving an inverse eigenvalue problem with triple constraints on eigenvalues, singular values, and diagonal elements.
Inverse Problems,
Vol. 33,
Issue. 8,
p.
085003.
Wang, Yi
and
Zheng, Sainan
2019.
The converse of Weyl's eigenvalue inequality.
Advances in Applied Mathematics,
Vol. 109,
Issue. ,
p.
65.