Published online by Cambridge University Press: 20 November 2018
The existence of certain formulae analogous to Poisson's summation formula (9, pp. 60-64),
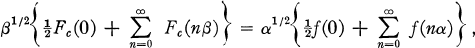
where αβ = 2π, α > 0, and Fc(x) is the Fourier cosine transform of f(x), but involving number-theoretic functions as coefficients, was first demonstrated by Voronoï (10) in 1904. He proved that
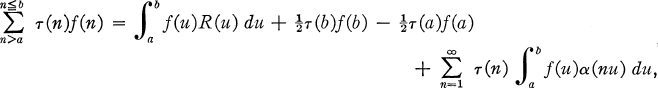
where r(n) is an arithmetic function,/(x) is continuous in (a, b) and a(x) and i?(x) are analytic functions dependent on τ(n). Later, numerous papers were published by various authors giving formulae of this type involving d(n), the number of divisors of n (3), and rp(n), the number of ways of expressing n as the sum of p squares of integers (8).
In 1937, Ferrar (4) developed a general theory of summation formulae, using complex analysis. Around that time, Guinand (5) also published papers where he developed the general theory from a different point of view. He applied the theory of mean convergence for the transforms of class L2(0, ∞ ). Later in 1950, Bochner (1) gave a general summation formula.