Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-15T09:55:58.432Z Has data issue: false hasContentIssue false
  • English
  • Français

Sur Les Representations Unitaires des Groupes de Lie Nilpotents. VI

Published online by Cambridge University Press:  20 November 2018

Jacques Dixmier
Jacques Dixmier*
Affiliation:
Institut Henri Poincaré
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Soient Γ un groupe localement compact, 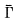l'ensemble des classes de représentations unitaires irréductibles de Γ. Dans (4), Godement a défini une topologie sur 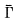que nous appellerons "topologie canonique." Cette topologie est facile à étudier lorsque Γ est abélien ou compact, mais fort mal connue en général. Dans un article récent (3), Fell a repris l'étude de la topologie canonique de 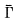, et réussi à la calculer lorsque Γ est le groupe spécial linéaire complexe à n variables. L'espace 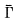est alors "presque" séparé, et, par suite, "presque" localement compact.

Il semble nécessaire d'étudier complètement quelques cas particuliers avant d'entreprendre une théorie générale de .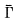

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 12 , 1960 , pp. 324 - 352
Copyright
Copyright © Canadian Mathematical Society 1960

References

1. Dixmier, J., Sur les représentations unitaires des groupes de Lie nilpotents. III, Can. J. Math., 10 (1958), 321–348.Google Scholar
2. Dixmier, J., Sur les représentations unitaires des groupes de Lie nilpotents. V, Bull. Soc. Math. France, 87 (1959), 65–79.Google Scholar
3. Fell, J.M.G., The dual spaces of C*-algebras, à paraître aux Trans. Amer. Math. Soc.Google Scholar
4. Godement, R., Les fonctions de type positif et la théorie des groupes, Trans. Amer. Math. Soc, 63 (1948), 1–84.Google Scholar