Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T10:40:31.900Z Has data issue: false hasContentIssue false
  • English
  • Français

Surfaces with pg = q = 2, K2 = 6, and Albanese Map of Degree 2

Published online by Cambridge University Press:  20 November 2018

Matteo Penegini  and
Francesco Polizzi
Matteo Penegini
Affiliation:
Lehrstuhl Mathematik VIII, Universität Bayreuth, NWII, D-95440 Bayreuth, Germany, e-mail: matteo.penegini@uni-bayreuth.de
Francesco Polizzi
Affiliation:
Dipartimento di Matematica, Università della Calabria, Cubo 30B, 87036, Arcavacata di Rende (Cosenza), Italy, e-mail: polizzi@mat.unical.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We classify minimal surfaces of general type with ${{p}_{g}}=q=2$ and ${{K}^{2}}=6$ whose Albanese map is a generically finite double cover. We show that the corresponding moduli space is the disjoint union of three generically smooth irreducible components 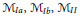${{\mathcal{M}}_{Ia}},\,{{\mathcal{M}}_{Ib}},\,{{\mathcal{M}}_{II}}$ of dimension 4, 4, 3, respectively.

Keywords

14J2914J10surface of general typeabelian surfaceAlbanese map
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 65 , Issue 1 , 01 February 2013 , pp. 195 - 221
Copyright
Copyright © Canadian Mathematical Society 2013

References

[Ba87] Barth, W., Abelian surfaces with (1, 2)-polarization. In: Algebraic geometry, Sendai, 1985, Adv. Stud. Pure Math., 10, North-Holland, Amsterdam, 1987, pp. 41–84.Google Scholar
[BHPV03] Barth, W., Hulek, K., Peters, C. A. M., and Van de Ven, A., Compact complex surfaces. Second ed. Ergebnisse der Mathematik und ihrer Grenzgebiete, 3, Folge. A Series of Modern Surveys in Mathematics, 4, Springer-Verlag, Berlin, 2004.Google Scholar
[BPS09] Bastianelli, F., Pirola, G. P., and Stoppino, L., Galois closure and Lagrangian varieties. Adv. Math. 225(2010), no. 6, 3463–3501. http://dx.doi.org/10.1016/j.aim.2010.06.006 Google Scholar
[BL04] Birkenhake, C. and Lange, H., Complex abelian varieties. Second ed., Grundlehren der MathematischenWissenschaften, 302, Springer-Verlag, Berlin, 2004.Google Scholar
[Ca90] Catanese, F., Footnotes to a theorem of I. Reider. In: Algebraic geometry (L'Aquila, 1988), Lecture Notes in Math., 1417, Springer, Berlin, 1990, pp. 67–74.Google Scholar
[Ca91] Catanese, F., Moduli and classification of irregular Kaehler manifolds (and algebraic varieties) with Albanese general type fibrations. Invent. Math. 104(1991), no. 2, 263–289. http://dx.doi.org/10.1007/BF01245076 Google Scholar
[Ca11] Catanese, F., A superficial working guide to deformations and moduli, arxiv:1106.1368, to appear in the Handbook of Moduli, a volume in honour of David Mumford, to be published by International Press.Google Scholar
[F98] Friedman, R., Algebraic surfaces and holomorphic vector bundles. Universitext, Springer-Verlag, New York, 1998.Google Scholar
[GAP4] The GAP Group, GAP - Groups, algorhithms, and programming, Version 4.4.12, 2008 http://www.gap-system.org. Google Scholar
[HP02] Hacon, C. D. and Pardini, R., Surfaces with pg = q = 3. Trans. Amer. Math. Soc. 354(2002), no. 7, 2631–2638. http://dx.doi.org/10.1090/S0002-9947-02-02891-X Google Scholar
[Har79] Harris, J., Galois groups of enumerative problems. Duke Math. J. 46(1979), no. 4, 685–724. http://dx.doi.org/10.1215/S0012-7094-79-04635-0 Google Scholar
[HvM89] Horozov, E. and van Moerbeke, P., The full geometry of Kowalewski's top and (1, 2)-abelian surfaces. Comm. Pure Appl. Math. 42(1989), no. 4, 357–407. http://dx.doi.org/10.1002/cpa.3160420403 Google Scholar
[Man08] M. Manetti, , Smoothing of singularities and deformation types of surfaces. In: Symplectic 4-manifolds and algebraic surfaces, Lecture Notes in Math., 1938, Springer, Berlin, 2008, pp. 169–230.Google Scholar
[Mu81] Mukai, S., Duality between D(X) and D() with its application to Picard sheaves. Nagoya Math. J. 81(1981), 153–175.Google Scholar
[Mu99] Mukai, S., Moduli of abelian surfaces and regular polyhedral groups. In Moduli of algebraic varieties and the monster, Proceedings, Sapporo, January 1999. Ed. I. Nakamura, Hokkaido Univ. 1999, pp. 68–74.Google Scholar
[Pe11] Penegini, M., The classification of isotrivially fibred surfaces with pg= q = 2. with an appendix by S. Roellenske. Collect. Math. 62(2011), no. 3, 239–274. http://dx.doi.org/10.1007/s13348-011-0043-y Google Scholar
[PP10] Penegini, M. and Polizzi, F., On surfaces with pg = q = 2, K2 = 5 and Albanese map of degree 3. arxiv:1011.4388. Google Scholar
[Pi02] Pirola, G. P., Surfaces with pg = q = 3. Manuscripta Math. 108(2002), no. 2, 163–170. http://dx.doi.org/10.1007/s002290200253 Google Scholar
[Rol10] Rollenske, S., Compact moduli for certain Kodaira fibrations. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 9(2010), no. 4, 851–874.Google Scholar
[Se06] Sernesi, E., Deformations of algebraic schemes. Grundlehren der Mathematischen Wissenschaften, 334, Springer-Verlag, Berlin, 2006.Google Scholar
[Z03] Zucconi, F., Surfaces with pg = q = 2 and an irrational pencil. Canad. J. Math. 55(2003), no. 3, 649–672. http://dx.doi.org/10.4153/CJM-2003-027-8 Google Scholar