Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T07:11:01.444Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetric Genuine Spherical WhittakerFunctions on

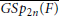
Published online by Cambridge University Press:  20 November 2018

Dani Szpruch
Dani Szpruch*
Affiliation:
Department of Mathematics, Purdue University, West Lafayette, IN 47907, USA. e-mail: dszpruch@math.purdue.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 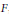$F$ be a p-adic field of odd residual characteristic. Let 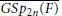$\overline{GS{{p}_{2n}}(F)}$ and 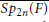$\overline{S{{p}_{2n}}(F)}$ be the metaplectic double covers of the general symplectic group and the symplectic group attached to the 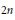$2n$ dimensional symplectic space over 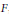$F$, respectively. Let 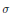$\sigma$ be a genuine, possibly reducible, unramified principal series representation of 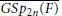$\overline{GS{{p}_{2n}}(F)}$. In these notes we give an explicit formula for a spanning set for the space of Spherical Whittaker functions attached to 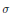$\sigma$. For odd $n$, and generically for even $n$, this spanning set is a basis. The significant property of this set is that each of its elements is unchanged under the action of the Weyl group of 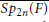$\overline{S{{p}_{2n}}(F)}$. If $n$ is odd, then each element in the set has an equivariant property that generalizes a uniqueness result proved by Gelbart, Howe, and Piatetski-Shapiro.Using this symmetric set, we construct a family of reducible genuine unramified principal series representations that have more then one generic constituent. This family contains all the reducible genuine unramified principal series representations induced from a unitary data and exists only for $n$ even.

Keywords

11F85metaplectic groupCasselman Shalika Formula
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 1 , 01 February 2015 , pp. 214 - 240
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Banks, W. D., Exceptional representations on the metaplectic group. Ph.D. Thesis, Stanford University. ProQuest LLC, Ann Arbor, MI, 1994.Google Scholar
[2] Bump, D., Automorphic forms and representations. Cambridge Studies in Advanced Mathematics, 55, Cambridge University Press, Cambridge, 1997.Google Scholar
[3] Bump, D., Friedberg, S., and Hoffstein, J., p-adic Whittaker functions on the metaplectic group. Duke Math. J. 63(1991), no. 2, 379–397.http://dx.doi.org/10.1215/S0012-7094-91-06316-7 Google Scholar
[4] Bernstein, I. N. and Zelevinsky, A. V., Representations of the group GL(n; F) where F is a non-archimedean local field. Russian Math. Surveys 31(1976), 1–68.Google Scholar
[5] Casselman, W. and Shalika, J., The unramified principal series of p-adic groups. II. The Whittaker function. Compositio Math. 41(1980), no. 2, 207–231.Google Scholar
[6] Chinta, G. and Offen, O., A metaplectic Casselman-Shalika formula for GL(r). Amer. J. Math. 135(2013), no. 2, 403–441.http://dx.doi.org/10.1353/ajm.2013.0013 Google Scholar
[7] Gan, W. T. and Savin, G., Representations of metaplectic groups I: epsilon dichotomy and local Langlands correspondence. Compositio Math. 148(2012), no. 6, 1655–1694.http://dx.doi.org/10.1112/S0010437X12000486 Google Scholar
[8] Gelbart, S., Howe, R., Piatetski-Shapiro, I. , Uniqueness and existence of Whittaker models for the metaplectic group. Israel J. Math. 34(1979), no. 1–2, 21–37.http://dx.doi.org/10.1007/BF02761822 Google Scholar
[9] Gelbart, S. and Piatetski-Shapiro, I., Some remarks on metaplectic cusp forms and the correspondences of Shimura and Waldspurger. Israel J. Math. 44(1983), no. 2, 97–126.http://dx.doi.org/10.1007/BF02760615 Google Scholar
[10] Hanzer, M. and Matic, I., Irreducibility of the unitary principal series of p-adic . Manuscripta, Math. 132(2010), no. 3-4, 539–547. http://dx.doi.org/10.1007/s00229-010-0362-4 Google Scholar
[11] Kazhdan, D. A. and Patterson, S. J., Metaplectic forms. Inst. Hautes Études Sci. Publ. Math. 59(1984) 35–142.Google Scholar
[12] Keys, C. D. and Shahidi, F., Artin L-functions and normalization of intertwining operators. Ann. Sci. École Norm. Sup. (4) 21(1988), no. 1, 67–89.Google Scholar
[13] McNamara, P. J., Principal series representations of metaplectic groups over local fields. In: Multiple Dirichlet series, L-functions and automorphic forms, Progr. Math., 300, Birkhäuser/Springer, New York, 2012.Google Scholar
[14] Moeglin, C., Vignéras, M.-F., and Waldspurger, J. L., Correspondances de Howe sur un corps p-adique. Lecture Notes in Mathematics, 1291, Springer-Verlag, Berlin, 1987.Google Scholar
[15] Moeglin, C. and Waldspurger, J. L., Spectral decomposition and Eisenstein series. Cambridge Tracts in Mathematics, 113, Cambridge University Press, Cambridge, 1995.Google Scholar
[16] Rao, R. R., On some explicit formulas in the theory of Weil representation. Pacific J. Math. 157(1993), no. 2, 335–371.http://dx.doi.org/10.2140/pjm.1993.157.335 Google Scholar
[17] Roberts, B., The theta correspondence for similitudes. Israel J. Math. 94(1996), 285–317.http://dx.doi.org/10.1007/BF02762709 Google Scholar
[18] Shahidi, F., On certain L-functions. Amer. J. Math. 103(1981), no. 2, 297–355.http://dx.doi.org/10.2307/2374219 Google Scholar
[19] Szpruch, D., Uniqueness of Whittaker model for the metaplectic group. Pacific J. Math. 232(2007), no. 2, 453–469.http://dx.doi.org/10.2140/pjm.2007.232.453 Google Scholar
[20] Szpruch, D., Computation of the local coefficients for principal series representations of the metaplectic double cover of SL2(F). J. Number Theory,129(2009), no. 9, 2180–2213.http://dx.doi.org/10.1016/j.jnt.2009.01.024 Google Scholar
[21] Szpruch, D., Some irreducibility theorems of parabolic induction on the metaplectic group via the Langlands-Shahidi method. Israel J. Math. 195(2013), no. 2, 897–971.http://dx.doi.org/10.1007/s11856-012-0140-y Google Scholar
[22] Szpruch, D., Some results in the theory of genuine representations of the metaplectic double cover of GSp(2,F) over p-adic fields. J. Algebra 388(2013), 160–193.http://dx.doi.org/10.1016/j.jalgebra.2013.05.001 Google Scholar
[23] Weil, A., Sur certains groupes d’op´erateurs unitaires. Acta Math 111(1964), 143–211.http://dx.doi.org/10.1007/BF02391012 Google Scholar