Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T05:12:26.588Z Has data issue: false hasContentIssue false
  • English
  • Français

The Symplectic Geometry of Polygons in the 3-Sphere

Published online by Cambridge University Press:  20 November 2018

Thomas Treloar
Thomas Treloar*
Affiliation:
Department of Mathematics University of Arizona Tucson, Arizona 85721 U.S.A., email: treloar@math.arizona.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the symplectic geometry of the moduli spaces 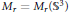${{M}_{r}}={{M}_{r}}\left( {{\mathbb{S}}^{3}} \right)$ of closed $n$-gons with fixed side-lengths in the 3-sphere. We prove that these moduli spaces have symplectic structures obtained by reduction of the fusion product of $n$ conjugacy classes in 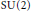$\text{SU}\left( 2 \right)$ by the diagonal conjugation action of 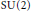$\text{SU}\left( 2 \right)$. Here the fusion product of $n$ conjugacy classes is a Hamiltonian quasi-Poisson 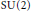$\text{SU}\left( 2 \right)$-manifold in the sense of 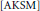$\left[ \text{AKSM} \right]$. An integrable Hamiltonian system is constructed on 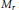${{M}_{r}}$ in which the Hamiltonian flows are given by bending polygons along a maximal collection of nonintersecting diagonals. Finally, we show the symplectic structure on 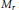${{M}_{r}}$ relates to the symplectic structure obtained from gauge-theoretic description of 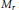${{M}_{r}}$. The results of this paper are analogues for the 3-sphere of results obtained for 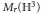${{M}_{r}}\left( {{\mathbb{H}}^{3}} \right)$, the moduli space of $n$-gons with fixed side-lengths in hyperbolic 3-space 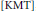$\left[ \text{KMT} \right]$, and for 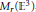${{M}_{r}}\left( {{\mathbb{E}}^{3}} \right)$, the moduli space of $n$-gons with fixed side-lengths in 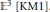${{\mathbb{E}}^{3}}\left[ \text{KM}1 \right]$.

Keywords

53D
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 54 , Issue 1 , 01 February 2002 , pp. 30 - 54
Copyright
Copyright © Canadian Mathematical Society 2002

References

[A] Alekseev, A., On Poisson actions of compact Lie groups on symplectic manifolds. J. Differential Geom. 45 (1997), 241–256.Google Scholar
[AKS] Alekseev, A. and Kosmann-Schwarzbach, Y., Manin pairs and moment maps. preprint, math.DG/9909176.Google Scholar
[AKSM] Alekseev, A., Kosmann-Schwarzbach, Y. and Meinrenken, E., Quasi-Poisson Manifolds. Canad. J. Math., this issue, 3–29.Google Scholar
[AMM1] Alekseev, A., Malkin, A. and Meinrenken, E., Lie group valued moment maps. J. Differential Geom. 48 (1998), 445–495.Google Scholar
[AMM2] Alekseev, A., Malkin, A. and Meinrenken, E., Manin pairs of a compact simple Lie algebra. unpublished notes.Google Scholar
[Bi] Birman, J., Braids, links, and mapping class groups. Ann. of Math. Studies 82, Princeton Univ. Press, 1974.Google Scholar
[CP] Chari, V. and Pressley, A., A Guide to Quantum Groups. Cambridge Univ. Press, 1994.Google Scholar
[FM] Flaschka, H. and Millson, J. J., On the moduli space of n points in . in preparation.Google Scholar
[Ga] Galitzer, A., The moduli space of polygon linkages in the 2-sphere. Ph.D. thesis, University of Maryland, 1997.Google Scholar
[Go] Goldman, W., Invariant functions on Lie groups and Hamiltonian flows of surface group representations. Invent. Math. 85 (1986), 263–302.Google Scholar
[GHJW] Guruprasad, K., Huebshmann, J., Jeffrey, L. and Weinstein, A., Group systems, groupoids, and moduli spaces of parabolic bundles. Duke Math. J. 89 (1997), 377–412.Google Scholar
[HK] Hausmann, J.-C. and Knutson, A., Polygon spaces and Grassmannians. Enseign. Math. (2) 43 (1997), 173–198.Google Scholar
[Je] Hausmann, J.-C. and Knutson, A., Extended moduli spaces of flat connections on Riemann surfaces. Math. Ann. 298 (1994), 667–692.Google Scholar
[JW] Jeffrey, L. and Weitsman, J., Torus actions, moment maps, and the moduli space of flat connections on a two-manifold. Contemp. Math. 175 (1994), 49–59.Google Scholar
[KM1] Kapovich, M. and Millson, J. J., The symplectic geometry of polygons in Euclidean space. J. Differential Geom. 44 (1996), 479–513.Google Scholar
[KM2] Kapovich, M. and Millson, J. J., The relative deformation theory of representations of flat connections and deformations of linkages in constant curvature spaces. Compositio Math. 103 (1996), 287–317.Google Scholar
[KM3] Kapovich, M. and Millson, J. J., On the moduli space of a spherical polygonal linkage. Canad. Math. Bull. 42 (1999), 307–320.Google Scholar
[KMT] Kapovich, M., Millson, J. J. and Treloar, T., The symplectic geometry of polygons in hyperbolic 3-space. Asian J. Math 4 (2000), 123–164.Google Scholar
[KS2] Kosmann-Schwarzbach, Y., Jacobian quasi-bialgebras and quasi-Poisson Lie groups. Contemp. Math. 132 (1991), 459–489.Google Scholar
[LM] Leeb, B. and Millson, J. J., Convex functions on symmetric spaces and geometric invariant theory for weighted configurations in flag manifolds. in preparation.Google Scholar
[Le] Leingang, M., Symmetric pairs and moment spaces, math.SG/9810064, preprint.Google Scholar
[Lu3] Lu, J.-H., Momentum mappings and reduction of Poisson actions. In: Symplectic Geometry, Groupoids, and Integable Systems, MSRI Publ. 20, Springer-Verlag, New York, 1991, 209–226.Google Scholar
[Mi] Millson, J. J., Bending polygons and decomposing tensor products, three examples. in preparation.Google Scholar
[Mo] Moser, J., On the volume elements on a manifold. Trans. Amer. Math. Soc. 120 (1965), 286–294.Google Scholar
[MZ] Millson, J. J. and Zombro, B., A Kähler structure on the moduli space of isometric maps of a circle into Euclidean space. Invent. Math. 123 (1996), 35–59.Google Scholar
[Sa] Sargent, M., Diffeomorphism equivalence of configuration spaces of polygons in constant curvature spaces. Ph.D. thesis, University of Maryland, 1995.Google Scholar
[STS] Semenov-Tian-Shansky, M., Dressing transformations and Poisson group actions. Publ. Res. Inst. Math. Sci. 21 (1985), 1237–1260.Google Scholar
[Th] Thurston, W., Three-dimensional geometry and topology. Princeton Univ. Press, 1997.Google Scholar
[Tr1] Treloar, T., Integrable hamiltonian systems on moduli spaces of polygonal linkages. Ph.D. thesis, University of Maryland, 2001.Google Scholar
[Tr2] Treloar, T., The symplectic geometry on loops in the 3-sphere. in preparation.Google Scholar