Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-16T01:01:49.517Z Has data issue: false hasContentIssue false
  • English
  • Français

Szegö Polynomials on a Compact Group with Ordered Dual

Published online by Cambridge University Press:  20 November 2018

I. I. Hirschman Jr.
I. I. Hirschman Jr.*
Affiliation:
Stanford University and Washington University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Szegö polynomials are defined on T, the real numbers modulo 1. In this paper and in its sequel we give a generalization of Szegö polynomials in which T is replaced by an arbitrary locally compact abelian group θ on whose dual 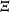there has been distinguished a measurable order relation compatible with the group structure. The present paper is devoted to the case where θ is compact and 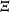therefore discrete. The general case will be taken up in the sequel mentioned above. It is desirable to proceed in this way because the case θ compact is much simpler and much more like the classical situation than is the general case, in which various measure-theoretic difficulties obtrude. Moreover, as it happens, it is possible to develop the theory in this way with relatively little repetition.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 18 , 1966 , pp. 538 - 560
Copyright
Copyright © Canadian Mathematical Society 1966

References

1. Baxter, G., Polynomials defined by a difference system, J. Math. Anal. Appl., 2 (1961), 223–263.Google Scholar
2. Baxter, G., A convergence equivalence related to polynomials on the unit circle, Trans. Amer. Math. Soc, 99 (1961), 471–487.Google Scholar
3. Baxter, G., A norm inequality for a “finite section” Wiener-Hopf equation, Illinois J. Math. 7, (1963), 97–103.Google Scholar
4. Baxter, G. and Hirschman, I. I. Jr., An explicit inversion formula for finite section Wiener-Hopf operators, Bull. Amer. Math. Soc, 70 (1964), 820–823.Google Scholar
5. Hirschman, I. I., Finite sections of Wiener-Hopf equations and Szegö polynomials, J. Math. Anal. Appl., 11 (1965), 290–320.Google Scholar
6. Hirschman, I. I., On a theorem of Szegö, Kac, and Baxter, J. Analyse Math., 14 (1965), 225–234.Google Scholar
7. Hirschman, I. I., Finite section Wiener-Hopf equations on a compact group with ordered dual, Bull. Amer. Math. Soc., 70 (1964), 508–510.Google Scholar
8. Shinbrot, M., A class of difference kernels, Proc. Amer. Math. Soc, 13 (1962), 399–406.Google Scholar