Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T09:23:04.209Z Has data issue: false hasContentIssue false
  • English
  • Français

Tannakian Categories With SemigroupActions

Published online by Cambridge University Press:  20 November 2018

Alexey Ovchinnikov  and
Michael Wibmer
Alexey Ovchinnikov
Affiliation:
CUNY Queens College, Department of Mathematics, 65-30 Kissena Blvd, Queens, NY 11367, USAand , CUNY Graduate Center, Department of Mathematics,365 Fifth Avenue, New York, NY 10016, USA e-mail: aovchinnikov@qc.cuny.edu
Michael Wibmer
Affiliation:
RWTH Aachen, 52056, Aachen, Germany and , University of Pennsylvania, Department of Mathematics, 209 South 33rd Street, Philadelphia, PA 19104, USA e-mail: wibmer@math.upenn.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A theorem of Ostrowski implies that 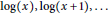$\log \left( x \right),\,\log \left( x+1 \right),\,.\,.\,.$ are algebraically independent over 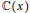$\mathbb{C}\left( x \right)$. More generally, for a linear differential or difference equation, it is an important problem to find all algebraic dependencies among a non-zero solution $y$ and particular transformations of $y$, such as derivatives of $y$ with respect to parameters, shifts of the arguments, rescaling, etc. In this paper, we develop a theory of Tannakian categories with semigroup actions, which will be used to attack such questions in full generality, as each linear differential equation gives rise to a Tannakian category. Deligne studied actions of braid groups on categories and obtained a finite collection of axioms that characterizes such actions to apply them to various geometric constructions. In this paper, we find a finite set of axioms that characterizes actions of semigroups that are finite free products of semigroups of the form 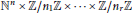${{\mathbb{N}}^{n}}\,\times \,\mathbb{Z}/{{n}_{1}}\mathbb{Z}\,\times \,.\,.\,.\,\mathbb{Z}/{{n}_{r}}\mathbb{Z}$ on Tannakian categories. This is the class of semigroups that appear in many applications.

Keywords

18D1012H1020G0533C0533C8034K06semigroup actions on categoriesTannakian categoriesdifference algebraic groupsdifferential and difference equations with parameters
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 3 , 01 June 2017 , pp. 687 - 720
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Baumslag, G. and Solitar, D., Some two-generator one relator non-Hopfian groups. Bull. Amer. Math. Soc. 68(1962), 199–201.http://dx.doi.org/10.1090/S0002-9904-1962-10745-9 Google Scholar
[2] Cohn, R. M., Difference algebra. Interscience Publishers, New York, 1965.Google Scholar
[3] Deligne, P., Catégories tannakiennes. In: The Grothendieck Festschrift. II. Progr. Math. 87, Birkhäuser Boston, Boston, MA, 1990, pp. 111–195.http://dx.doi.Org/10.1007/978-0-81 76-4575-5_3 Google Scholar
[4] Deligne, P., Action du groupe des tresses sur une catégorie. Invent. Math. 128(1997), 159–175. http://dx.doi.org/10.1007/s002220050138 Google Scholar
[5] Deligne, P. and Milne, J., Tannakian categories. In: Hodge cycles, motives, and Shimura varieties. Lecture Notes in Mathematics, 900. Springer-Verlag, Berlin, 1982, pp. 101–228. http://www.jmilne.org/math/xnotes/tc.pdf. Google Scholar
[6] Di Vizio, L, Hardouin, C. , and Wibmer, M., Difference Galois theory of linear differential equations. Adv. Math. 260(2014), 1–58.http://dx.doi.org/10.1016/j.aim.2o14.04.005 Google Scholar
[7] Di Vizio, L, Difference algebraic relations among solutions of linear differential equations. J. Inst. Math. Jussieu 2016.http://dx.doi.Org/10.101 7/S147474801 5000080 Google Scholar
[8] Drinfeld, V., Gelaki, S., Nikshych, D., and Ostrik, V., On braided fusion categories. I. Selecta Math. (N.S.) 16(2010), no. 1,1–119.http://dx.doi.org/10.1007/s00029-010-001 7-z Google Scholar
[9] Frenkel, E., Langlands correspondence for loop groups. Cambridge Studies in Advanced Mathematics, 103. Cambridge University Press, Cambridge, 2007.http://math.berkeley.edu/-frenkel/loop.pdf. Google Scholar
[10] Gillet, H., Gorchinskiy, S., andOvchinnikov, A., Parameterized Picard-Vessiot extensions and Atiyah extensions. Adv. Math. 238(2013), 322–411.http://dx.doi.Org/10.1016/j.aim.2013.02.006 Google Scholar
[11] Kamensky, M., Tannakian formalism over fields with operators. Internat. Math. Res. Notices 24(2013), 5571–5622.http://dx.doi.Org/10.1093/imrn/rns190 Google Scholar
[12] Kamensky, M., Model theory and the Tannakian formalism. Trans. Amer. Math. Soc. 367(2015)1095–1120.http://dx.doi.org/10.1090/S0002-9947-2014-06062-5 Google Scholar
[13] Koornwinder, T. H., Group theoretic interpretations of Askey's scheme of hypergeometric orthogonal polynomials. In: Orthogonal polynomials and their applications. Lecture Notes in Mathematics, 1329. Springer, 1988, pp. 46–72.http://dx.doi.Org/10.1 OO7/BFbOO83353 Google Scholar
[14] Levin, A., Difference algebra. Algebra and Applications, 8. Springer, New York, 2008.http://dx.doi.org/10.1007/978-1-4020-6947-5 Google Scholar
[15] Mac Lane, S., Categories for the working mathematician. Springer, New York, 1978.http://dx.doi.org/10.1007/978-1-4757-4721-8 Google Scholar
[16] Minchenko, A. and Ovchinnikov, A., Zariski closures of reductive linear differential algebraic groups. Adv. Math. 227(2011), no. 3, 1195–1224.http://dx.doi.Org/10.1016/j.aim.2O11.03.002 Google Scholar
[17] Minchenko, A., Ovchinnikov, A., and Singer, M. F., Unipotent differential algebraic groups as parameterized differential Galois groups. J. Inst. Math. Jussieu 13(2014), no. 4, 671–700.http://dx.doi.Org/10.1017/S1474748013000200 Google Scholar
[18] Ostrowski, A., Sur les relations algébriques entre les intégrales indéfinies. Acta Math. 78(1946), no. 1,315–318.http://dx.doi.org/10.1007/BF02421605 Google Scholar
[19] Ovchinnikov, A., Tannakian approach to linear differential algebraic groups. Transform. Groups 13(2008), no. 2, 413–446.http://dx.doi.org/10.1007/s00031-008-9010-4 Google Scholar
[20] Ovchinnikov, A., Tannakian categories, linear differential algebraic groups, and parametrized linear differential equations. Transform. Groups 14(2009), no. 1,195–223.http://dx.doi.org/10.1007/s00031-008-9042-9 Google Scholar
[21] Ovchinnikov, A., Differential Tannakian categories. J. Algebra 321(2009), no. 10, 3043–3062. http://dx.doi.Org/10.1016/j.jalgebra.2OO9.O2.008 Google Scholar
[22] Ovchinnikov, A., Difference integrability conditions for parameterized linear difference and differential equations. Adv. Appl. Math. 53(2014), 61–71.http://dx.doi.Org/10.1016/j.aam.2013.09.007 Google Scholar
[23] Ovchinnikov, A. and Wibmer, M., a-Galois theory of linear difference equations. Internat. Math. Res. Notices 2015 (12): 3962–4018, 2015.http://dx.doi.Org/10.1093/imrn/rnu060 Google Scholar
[24] Saavedra Rivano, N., Catégories Tannakiennes. Lecture Notes in Mathematics, 265. Springer-Verlag, Berlin, 1972. http://dx.doi.Org/10.1OO7/BFbOO59108 Google Scholar
[25] van der Put, M. and Singer, M. F., Galois theory of linear differential equations. Fundamental Principles of Mathematical Sciences, 328. Springer-Verlag, Berlin, 2003.http://dx.doi.org/10.1007/978-3-642-55750-7 Google Scholar
[26] Vilenkin, N. J.and Klimyk, A. U., Representation of Lie groups and special functions. Simplest Lie Groups, Special Functions and Integral Transforms, vol. 1. Springer, Netherlands, 1991.http://dx.doi.org/10.1007/978-94-011-3538-2 Google Scholar
[27] Waterhouse, W. C., Introduction to affine group schemes. Graduate Texts in Mathematics, 66. Springer-Verlag, New York, 1979.http://dx.doi.org/10.1007/978-1-4612-6217-6 Google Scholar
[28] Wibmer, M., Existence of d-parameterized Picard-Vessiot extensions over fields with algebraically closed constants. J. Algebra 361(2012), 163–171.http://dx.doi.Org/10.1016/j.jalgebra.2012.03.035 Google Scholar