Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Diamond, Harold G.
1973.
Chebyshev estimates for Beurling generalized prime numbers.
Proceedings of the American Mathematical Society,
Vol. 39,
Issue. 3,
p.
503.
1975.
Abstract Analytic Number Theory.
Vol. 12,
Issue. ,
p.
297.


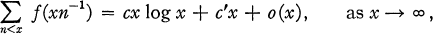
 , and uses Pitt's form of Wiener's Tauberian theorem; (see, e.g., 5, Theorem 109, p. 211).
, and uses Pitt's form of Wiener's Tauberian theorem; (see, e.g., 5, Theorem 109, p. 211).