Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-27T11:29:02.344Z Has data issue: false hasContentIssue false
  • English
  • Français

A Tauberian Theorem For The Riemann-Liouville Integral Of Integer Order

Published online by Cambridge University Press:  20 November 2018

C. T. Rajagopal
C. T. Rajagopal*
Affiliation:
Ramanujan Institute of Mathematics Madras, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1. Notation. Let s(x) be a function integrable in every finite interval of x ≥ 0. Then the Riemann-Liouville integral of s(x), of order a > 0, is defined for x ≥ 0 by

(1).

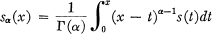The object of this note is to prove a Tauberian theorem for sα(x) in the case in which α is a positive integer p, employing certain difference formulae due to Karamata (4, Lemma 2) and Bosanquet (1, Theorem 1) used already for a broadly similar purpose in an earlier paper (12) where a is any positive number.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 9 , 1957 , pp. 487 - 499
Copyright
Copyright © Canadian Mathematical Society 1957

References

1. Bosanquet, L. S., Note on convexity theorems, J. London Math. Soc, 18 (1943), 239–248.Google Scholar
2. Doetsch, G., Ueber die Cesàrosche Summabilität bei Reihen und eine Erweiterung des Grenzwertbegriffs bei integrablen Funktionen, Math. Z., 11 (1921), 161–179.Google Scholar
3. Karamata, J., Beziehungen Zwischen den O sdilations grenzen einer Funktion und ihrer arithmetischen Mittel, Proc. London Math. Soc, (2) 43 (1937), 20–25.Google Scholar
4. Karamata, J., Quelques théorèmes inverses relatifs aux procédés de sommabilitié de Cesàro et Riesz, Acad. Serbe Sci. Publ. Inst. Math., 3 (1950), 53–71.Google Scholar
5. Obrechkoff, N., Sur un formule pour les différences divisées et sur les limites de fonctions et de leurs dérivées, C.R. Acad. Bulgare Sci., 2 (1949), 5–8.Google Scholar
6. Parthasarathy, M. and Rajagopal, C. T., A theorem on the Riemann-Liouville integral, Math. Z., 55 (1951), 84–91.Google Scholar
7. Pitt, H. R., A note on Tauberian conditions for Abel and Cesàro summability, Proc. Amer,. Math. Soc, 6 (1955), 616–619.Google Scholar
8. Rajagopal, C. T., A note on the oscillation of Riesz means of any order, J. London Math. Soc, 21 (1946), 275–282.Google Scholar
9. Rajagopal, C. T., On the limits of oscillation of a function and its Cesàro means, Proc. Edinburgh Math. Soc, (2) 7 (1946), 162–167.Google Scholar
10. Rajagopal, C. T., On some extensions of Ananda Rau's converse of Abel's theorem, J. London Math, Soc, 23 (1948), 38–44.Google Scholar
11. Rajagopal, C. T., On a Tauberian theorem of G. Ricci, Proc. Edinburgh Math. Soc, (2) 8 (1949), 143–146.Google Scholar
12. Rajagopal, C. T., On Tauberian theorems for the Riemann-Liouville integral, Acad. Serbe Sci. PubL Inst. Math., 6 (1954), 27–46.Google Scholar
13. Widder, D. V., The Laplace Transform (Princeton, 1941).Google Scholar