Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Milner, E. C.
and
Sauer, N.
1970.
GENERALIZATIONS OF A LEMMA OF FOLKMAN.
Annals of the New York Academy of Sciences,
Vol. 175,
Issue. 1,
p.
295.
Plummer, Michael D.
1970.
Some covering concepts in graphs.
Journal of Combinatorial Theory,
Vol. 8,
Issue. 1,
p.
91.
Milner, E. C.
and
Sauer, N.
1970.
GENERALIZATIONS OF A LEMMA OF FOLKMAN.
Annals of the New York Academy of Sciences,
Vol. 175,
Issue. 1 The Impac of,
p.
295.
Las Vergnas, Michel
1971.
Sur un problème de Erdös et Hajnal.
Journal of Combinatorial Theory, Series B,
Vol. 11,
Issue. 1,
p.
39.
1973.
Graphs and Hypergraphs.
Vol. 6,
Issue. ,
p.
498.
Wessel, W.
1975.
A first family of edge-critical wheels.
Periodica Mathematica Hungarica,
Vol. 6,
Issue. 3,
p.
229.
Greenwell, Don
1978.
Theory and Applications of Graphs.
Vol. 642,
Issue. ,
p.
191.
Berge, Claude
1978.
Advances in Graph Theory.
Vol. 3,
Issue. ,
p.
11.
Staples, Jo Ann W.
1979.
On some subclasses of well‐covered graphs.
Journal of Graph Theory,
Vol. 3,
Issue. 2,
p.
197.
Surányi, László
1980.
On a generalization of linecritical graphs.
Discrete Mathematics,
Vol. 30,
Issue. 3,
p.
277.
Berge, Claude
1981.
Graph Theory and Algorithms.
Vol. 108,
Issue. ,
p.
108.
Berge, Claude
1982.
Theory and Practice of Combinatorics - A collection of articles honoring Anton Kotzig on the occasion of his sixtieth birthday.
Vol. 60,
Issue. ,
p.
31.
Amahashi, Atsushi
and
Kano, Mikio
1982.
On factors with given components.
Discrete Mathematics,
Vol. 42,
Issue. 1,
p.
1.
Lovász, L.
1983.
Ear-decompositions of matching-covered graphs.
Combinatorica,
Vol. 3,
Issue. 1,
p.
105.
Koh, Khee Meng
and
Yap, Hian Poh
1984.
Graph Theory Singapore 1983.
Vol. 1073,
Issue. ,
p.
324.
Kano, Mikio
1986.
Factors of regular graphs.
Journal of Combinatorial Theory, Series B,
Vol. 41,
Issue. 1,
p.
27.
Hell, P.
and
Kirkpatrick, D. G.
1986.
Packings by Complete Bipartite Graphs.
SIAM Journal on Algebraic Discrete Methods,
Vol. 7,
Issue. 2,
p.
199.
1986.
Matching Theory.
Vol. 121,
Issue. ,
p.
483.
Füredi, Zoltán
1988.
Matchings and covers in hypergraphs.
Graphs and Combinatorics,
Vol. 4,
Issue. 1,
p.
115.
Tipnis, S. K.
and
Trotter, Jr., L. E.
1989.
Node-Packing Problems with Integer Rounding Properties.
SIAM Journal on Discrete Mathematics,
Vol. 2,
Issue. 3,
p.
407.
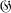 is considered to be an ordered pair 〈G,
is considered to be an ordered pair 〈G, 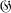 *〉 where G is a finite set the elements of which are called the vertices of
*〉 where G is a finite set the elements of which are called the vertices of 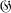 while
while 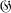 * is a subset of [G]2 (where [G]2 is the set of all subsets of two elements of G). The elements of
* is a subset of [G]2 (where [G]2 is the set of all subsets of two elements of G). The elements of 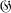 * are called the edges of
* are called the edges of 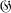 . If {P, Q} ∊
. If {P, Q} ∊ 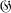 *, we say that Q is adjacent to P. The degree of a vertex is the number of vertices adjacent to it. Let k be an integer. We say that
*, we say that Q is adjacent to P. The degree of a vertex is the number of vertices adjacent to it. Let k be an integer. We say that 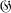 is the complete k-graph if G has k elements and
is the complete k-graph if G has k elements and 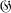 * = [G]2.
* = [G]2.