Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T13:35:04.005Z Has data issue: false hasContentIssue false
  • English
  • Français

Theta Lifts of Tempered Representations for Dual Pairs (Sp2n,O(V))

Published online by Cambridge University Press:  20 November 2018

Goran Muić
Goran Muić*
Affiliation:
Department of Mathematics, University of Zagreb, 10000 Zagreb, Croatia e-mail:gmuic@math.hr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

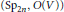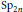This paper is the continuation of our previous work on the explicit determination of the structure of theta lifts for dual pairs $\left( {{\text{S}}_{{{\text{p}}_{2n}},}}\,O\left( V \right) \right)$ over a non-archimedean field $F$ of characteristic different than 2, where $n$ is the split rank of ${{\text{S}}_{{{\text{p}}_{2n}}}}$ and the dimension of the space 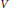$V$ (over $F$) is even. We determine the structure of theta lifts of tempered representations in terms of theta lifts of representations in discrete series.

Keywords

Primary 22E3secondary: 22E5011F70
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 6 , 01 December 2008 , pp. 1306 - 1335
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Bernstein, J., Second adjointness for representations of p-adic reductive groups. Preprint (Harvard 1987).Google Scholar
[2] Bernstein, I. N. and Zelevinsky, A. V., Induced representations of reductive p-adic groups. I. Ann. Sci.É cole Norm Sup. 10(1977), no. 4, 441–472.Google Scholar
[3] Casselman, W., Introduction to the theory of admissible representations of p-adic reductive groups. Preprint, www.math.ubc.ca/˜ cass/research/p-adic-book-dvi.Google Scholar
[4] Goldberg, D., Reducibility of induced representations for Sp(2n) and SO(n). Amer. J. Math. 116(1994), no. 5, 1101—1151.Google Scholar
[5] Kudla, S. S., On the local theta-correspondence. Invent. Math. 83(1986), no. 2, 229–255.Google Scholar
[6] Kudla, S. S., On the Theta Correspondence. (lectures at European School of Group Theory, Beilngries, 1996), www.math.toronto.ca/˜ skudla/castle/pdf.Google Scholar
[7] Lapid, E., Muić, G., and Tadić, M., On the generic unitary dual of quasi-split classical groups. Int. Math. Res. Not. 2004, no. 26, 1335–1354.Google Scholar
[8] Moeglin, C., Sur la classification des séries discrètes des groupes classiques p-adiques: paramètres de Langlands et exhaustivité. J. Eur. Math. Soc. (JEMS) 4(2002), no. 2, 143–200.Google Scholar
[9] Moeglin, C. and Tadić, M., Construction of discrete series for classical p-adic groups. J. Amer. Math. Soc 15(2005), no. 3, 715–786.Google Scholar
[10] Moeglin, C., Vignéras, M.-F., and Waldspurger, J.L., Correspondence de Howe sur un corps p-adique. Lecture Notes inMathematics 1291, Springer-Verlag, Berlin, 1987.Google Scholar
[11] Muić, G., Howe correspondence for discrete series representations; the case of (Sp(n),O(V)). J. Reine Angew. Math. 567(2004), 99–150.Google Scholar
[12] Muić, G., Reducibility of standard representations. Pacific J. Math. 222(2005), no. 1, 133–168.Google Scholar
[13] Muić, G., On the structure of the full lift for the Howe correspondence of (Sp(n),O(V)) for rank-one reducibilities. Canad. Math. Bull. 49(2006), no. 4, 578–591.Google Scholar
[14] Muić, G., On the structure of theta lifts of discrete series for dual pairs (Sp(n),O(V)). Israel J. Math. 164(2008), 87–124.Google Scholar
[15] Muić, G. and Savin, G., Symplectic-orthogonal theta lifts of generic discrete series. Duke Math. J. 101(2000), no. 2, 317–333.Google Scholar
[16] Rallis, S., On the Howe duality conjecture. CompositioMath. 51(1984), no. 3, 333–399.Google Scholar
[17] Tadić, M., On regular square integrable representations of p-adic groups. Amer. J. Math 120(1998), no. 1, 159–210.Google Scholar
[18] Waldspurger, J.-L., Démonstration d’une conjecture de duality de Howe dans le case p-adiques, p 6= 2. Festschrift in Honor of I.I. Piatetski-Shapiro, Part II, Israel Math. Conf. Proc. 2,Weizmann, Jerusalem, 1990, pp. 267–324.Google Scholar
[19] Waldspurger, J.-L., La formule de Plancherel pour les groupes p-adiques, d’après Harish-Chandra. J. Inst. Math. Jussieu 2(2003), no. 2, 235–333.Google Scholar
[20] Zelevinsky, A. V., Induced representations of reductive p-adic groups. II. On irreducible representations of GL(n). Ann. Sci. Ecole Norm. Sup. 13(1980), no. 2, 165–210.Google Scholar