Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T14:04:58.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Toric Geometry of SL2(ℂ) Free Group Character Varieties from Outer Space

Published online by Cambridge University Press:  20 November 2018

Christopher Manon
Christopher Manon*
Affiliation:
Department of Mathematics, George Mason University, Fairfax, VA 22030 USA e-mail: cmanon@gmu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Culler and Vogtmann defined a simplicial space 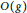$O\left( g \right)$, called outer space, to study the outer automorphism group of the free group 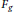${{F}_{g}}$. Using representation theoretic methods, we give an embedding of 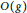$O\left( g \right)$ into the analytification of 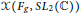$x\left( {{F}_{g}}\,,\,S{{L}_{2}}\left( \mathbb{C} \right) \right)$, the 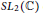$S{{L}_{2}}\left( \mathbb{C} \right)$ character variety of 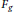${{F}_{g}}$, reproving a result of Morgan and Shalen. Then we show that every point $v$ contained in a maximal cell of 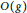$O\left( g \right)$ defines a flat degeneration of 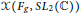$x\left( {{F}_{g}}\,,\,S{{L}_{2}}\left( \mathbb{C} \right) \right)$ to a toric variety 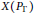$X\left( {{P}_{\Gamma }} \right)$. We relate 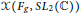$x\left( {{F}_{g}}\,,\,S{{L}_{2}}\left( \mathbb{C} \right) \right)$ and 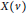$X\left( v \right)$ topologically by showing that there is a surjective, continuous, proper map 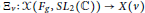${{\Xi }_{v}}\,:\,x\left( {{F}_{g}}\,,\,S{{L}_{2}}\,\left( \mathbb{C} \right) \right)\,\to \,X\left( v \right)$. We then show that this map is a symplectomorphism on a dense open subset of 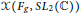$x\left( {{F}_{g}}\,,\,S{{L}_{2}}\left( \mathbb{C} \right) \right)$ with respect to natural symplectic structures on 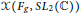$x\left( {{F}_{g}}\,,\,S{{L}_{2}}\left( \mathbb{C} \right) \right)$ and 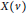$X\left( v \right)$. In this way, we construct an integrable Hamiltonian system in 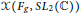$x\left( {{F}_{g}}\,,\,S{{L}_{2}}\left( \mathbb{C} \right) \right)$ for each point in a maximal cell of 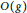$O\left( g \right)$, and we show that each $v$ defines a topological decomposition of 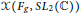$x\left( {{F}_{g}}\,,\,S{{L}_{2}}\left( \mathbb{C} \right) \right)$ derived from the decomposition of 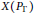$X\left( {{P}_{\Gamma }} \right)$ by its torus orbits. Finally, we show that the valuations coming from the closure of a maximal cell in 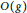$O\left( g \right)$ all arise as divisorial valuations built from an associated projective compactification of 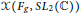$x\left( {{F}_{g}}\,,\,S{{L}_{2}}\left( \mathbb{C} \right) \right)$.

Keywords

14M2514T0514D20character varietyouter spaceanalytificationcompactificationintegrable system
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 2 , 01 April 2018 , pp. 354 - 399
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Alessandrini, D., Amoebas, tropical varieties and compactification of Teichmüller spaces. http://arxiv:math/0505269 Google Scholar
[2] Baez, J. C., An introduction to spin foam models ofBF theory and quantum gravity. In: Geometry and quantum physics (Schladming, 1999), Lecture Notes in Phys. , 543, Springer, Berlin, 2000, pp. 25–93.http://dx.doi.Org/10.1007/3-540-46552-9_2 Google Scholar
[3] Berkovich, V. G., Spectral theory and analytic geometry over non-Archimedean fields. Mathematical Surveys and Monographs , 33, American Mathematical Society, Providence, RI, 1990.Google Scholar
[4] Billera, L. J., Holmes, S. P., and Vogtmann, K., Geometry of the space of phylogenetic trees. Adv. in Appl. Math. 27(2001), no. 4, 733–767.http://dx.doi.Org/10.1006/aama.2001.0759 Google Scholar
[5] Culler, M. and Morgan, J. W., Group actions on R-trees. Proc. London Math. Soc. (3) 55(1987), no. 3, 571–604.http://dx.doi.Org/10.1112/plms/s3-55.3.571 Google Scholar
[6] Culler, M. and Vogtmann, K., Moduli of graphs and automorphisms of free groups. Invent. Math. 84(1986), no. 1, 91–119. http://dx.doi.Org/10.1007/BF01388734 Google Scholar
[7] Florentino, C. and Lawton, S., In the tradition of Ahlfors-Bers. VI. Contemp. Math. , 590, American Mathematical Society, Providence, RI, 2013, pp. 9–38.http://dx.doi.Org/10.1090/conm/590/11720 Google Scholar
[8] Gross, M., Hacking, P., Keel, S., and Kontsevich, M., Canonical bases for cluster algebras. http://arxiv:1411.1394 Google Scholar
[9] Guillemin, V., Jeffrey, L., and Sjamaar, R., Symplectic implosion. Transform. Groups 7(2002), no, 2, 155–184. http://dx.doi.Org/10.1007/s00031-002-0009-y Google Scholar
[10] Grosshans, F. D., Algebraic homogeneous spaces and invariant theory. Lecture Notes in Mathematics , 1673, Springe-Verlag, Berlin, 1997.Google Scholar
[11] Harada, M. and Kaveh, K., Toric degenerations, integrable systems and Okounkov bodies. Invent. Math., to appear. http://arxiv:1205.5249 http://dx.doi.org/10.1007/s00222-014-0574-4 Google Scholar
[12] Howard, B., Manon, C., and Millson, J., The toric geometry of triangulated polygons in Euclidean space. Canad. J. Math. 63(2011), no. 4, 878–937.http://dx.doi.Org/10.4153/CJM-2O11-021-0 Google Scholar
[13] Hilgert, J., Manon, C., and Martens, J., Contraction of Hamiltonian K-spaces. http://arxiv:1509.06406 Google Scholar
[14] Kirwan, F., Symplectic implosion and nonreductive quotients. In: Geometric aspects of analysis and mechanics, Progr. Math. , 292, Birkhäuser/Springer, New York, 2011, pp. 213–256.http://dx.doi.Org/10.1007/978-0-8176-8244-6_9 Google Scholar
[15] Kaveh, K. and Khovanskii, A. G., Newton-Okounkov bodies, semigroups of integral points, graded algebras and intersection theory. Ann. of Math. (2) 176(2012), no. 2, 925–978.http://dx.doi.Org/10.4007/annals.2012.176.2.5 Google Scholar
[16] Kempf, G. and Ness, L., The length of vectors in representation spaces. In: Algebraic geometry (Proc. Summer Meeting, Univ. Copenhagen, Copenhagen, 1978), Lecture Notes in Math. , 732, Springer, Berlin, 1979, pp. 233–243.Google Scholar
[17] Lawton, S. and Peterson, E., Spin networks and SL(2, ℂ)-character varieties. In: Handbook of Teichmüller theory. Vol. II, IRMA Lect. Math. Theor. Phys., 13, Eur. Math. Soc , Zürich, 2009, pp. 685–730. http://dx.doi.org/10.4171/055-1/17Google Scholar
[18] Manon, C., Symplectic geometry of the Vinberg monoid and branching problems. Mathematisches Forschungsinstitut Oberwolfach Report No. 27/2014, 31–35.http://dx.doi.Org/10.4171/OWR/2014/27 Google Scholar
[19] Manon, C., The algebra of conformai blocks. http://arxiv:0910.0577v6 Google Scholar
[20] Manon, C., Dissimilarity maps on trees and the representation theory of SLm(ℂ). J. Algebraic Combin. 33(2011), no. 2, 199–213.http://dx.doi.org/10.1007/s10801-010-0241-9 Google Scholar
[21] Manon, C., Compactifications of character varieties and skein relations on conformai blocks. Geom. Dedicata, to appear. http://arxiv:1401.8249 http://dx.doi.Org/10.1007/s10711-015-0084-6 Google Scholar
[22] Manon, C., Newton-Okounkovpolyhedra for character varieties and configuration spaces. http://arxiv:1403.3990 Google Scholar
[23] Morgan, J. W. and Shalen, P. B., Valuations, trees, and degenerations of hyperbolic structures. I. Ann. of Math. (2) 120(1984), no. 3, 401–476.http://dx.doi.org/10.2307/1971082 Google Scholar
[24] Maclagan, D. and Sturmfels, B., Introduction to tropical geometry. Graduate Studies in Mathematics , 161, American Mathematical Society, Providence, RI, 2015.Google Scholar
[25] Martens, J. and Thaddeus, M., On non-Abelian symplectic cutting. Transform. Groups 17(2012), no. 4, 1059–1084. http://dx.doi.org/10.1007/s00031-012-9202-9Google Scholar
[26] Nishinou, T., Nohara, Y., and Ueda, K., Toric degenerations of Gelfand-Cetlin systems and potential functions. Adv. Math. 224(2010), no. 2, 648–706.http://dx.doi.org/10.1016/j.aim.2009.12.012 Google Scholar
[27] Payne, S., Analytification is the limit of all tropicalizations. Math. Res. Lett. 16(2009), no. 3, 543–556. http://dx.doi.Org/10.4310/MRL.2OO9.v16.n3.a13 Google Scholar
[28] Procesi, C., The invariant theory of n × n matrices. Adv. in Math. 19(1976), 306–381.http://dx.doi.Org/10.1016/0001-8708(76)9002 7-X Google Scholar
[29] Ruan, W.-D., Lagrangian torus fibration ofquintic hypersurfaces. I. Fermat quintic case. In: Winter School on Mirror Symmetry, Vector Bundles and Lagrangian Submanifolds (Cambridge, MA, 1999), AMS/IP Stud. Adv. Math. , 23, American Mathematical Socieyu, Providence, RI, 2001, pp. 297–332.Google Scholar
[30] Sjamaar, R., Convexity properties of the moment mapping re-examined. Adv. Math. 138(1998), no. 1, 46–91.http://dx.doi.Org/10.1006/aima.1998.1739 Google Scholar
[31] Speyer, D. and Sturmfels, B., The tropical Grassmannian. Adv. Geom. 4(2004), no. 3, 389–411.http://dx.doi.Org/10.1515/advg.2004.023 Google Scholar
[32] Thurston, W. P., On the geometry and dynamics of diffeomorphisms of surfaces. Bull. Amer. Math. Soc. (N.S.) 19(1988), no. 2, 417–431.http://dx.doi.org/10.1090/S0273-0979-1988-15685-6 Google Scholar
[33] Vinberg, E. B., On reductive algebraic semigroups. In: Lie groups and Lie algebras: E. B. Dynkin's Seminar, Amer. Math. Soc. Transi. (2), 169, American Mathematical Society, Providence, RI , 1995, pp. 145–182.Google Scholar
[34] Vinberg, E. B., The asymptotic semigroup of a semisimple Lie group. In: Semigroups in algebra, geometry and analysis (Oberwolfach, 1993), de Gruyter Exp. Math., 20, de Gruyter , Berlin, 1995, pp. 293–310.Google Scholar
[35] Vogtmann, K., Automorphisms of free groups and outer space. In: Proceedings of the Conference on Geometric and Combinatorial Group Theory, Part I (Haifa, 2000), Geom. Dedicata 94(2002), 1–31.http://dx.doi.org/10.1023/A:1020973910646 Google Scholar