Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T23:47:51.690Z Has data issue: false hasContentIssue false
  • English
  • Français

The Toric Geometry of Triangulated Polygons in Euclidean Space

Published online by Cambridge University Press:  20 November 2018

Benjamin Howard ,
Christopher Manon  and
John Millson
Benjamin Howard
Affiliation:
Center for Communications Research, Princeton, NJ 08540, U.S.A. e-mail: bhoward73@gmail.com
Christopher Manon
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD 20742, U.S.A. e-mail: manonc@math.umd.edu jjm@math.umd.edu
John Millson
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD 20742, U.S.A. e-mail: manonc@math.umd.edu jjm@math.umd.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

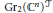Speyer and Sturmfels associated Gröbner toric degenerations $\text{G}{{\text{r}}_{2}}{{({{\mathbb{C}}^{n}})}^{\mathcal{T}}}$ of 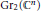$\text{G}{{\text{r}}_{2}}{{({{\mathbb{C}}^{n}})}^{{}}}$ with each trivalent tree 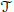$\mathcal{T}$ having $n$ leaves. These degenerations induce toric degenerations 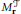$M_{r}^{\mathcal{T}}$ of 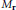${{M}_{r}}$, the space of $n$ ordered, weighted (by $\mathbf{r}$) points on the projective line. Our goal in this paper is to give a geometric (Euclidean polygon) description of the toric fibers and describe the action of the compact part of the torus as “bendings of polygons”. We prove the conjecture of Foth and Hu that the toric fibers are homeomorphic to the spaces defined by Kamiyama and Yoshida.

Keywords

14L2453D20
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 4 , 01 August 2011 , pp. 878 - 937
Copyright
Copyright © Canadian Mathematical Society 2011

References

[AB] Alexeev, V. and Brion, M., Toric degenerations of spherical varieties. Selecta Math. 10(2004), no. 4, 453–478.Google Scholar
[Bou1] Bourbaki, N., Commutative algebra. Chapters 1–7. Springer-Verlag, Berlin, 1998.Google Scholar
[BW] Buczyńska, W. and Wisńiewski, J., On geometry of binary symmetric models of phylogenetic trees. J. Eur. Math. Soc. 9(2007), no. 3, 609–635.Google Scholar
[CLO] Cox, D., Little, J., and O’Shea, D., Ideals, varieties, and algorithms. An introduction to computational algebraic geometry and commutative algebra. Undergraduate Texts in Mathematics, Springer-Verlag, New York, 1992.Google Scholar
[DM] Deligne, P. and Mostow, G. D., Monodromy of hypergeometric functions and nonlattice integral monodromy. Inst. Hautes Études Sci. Publ. Math. 63(1986), 5–89.Google Scholar
[dLMc] De Loera, J. A. and McAllister, T. B., Vertices of Gelfand-Tsetlin polytopes. Discrete Comput. Geom. 32(2004), no. 4, 459–470. doi:10.1007/s00454-004-1133-3Google Scholar
[Del] Delzant, T., Hamiltoniens périodiques et images convexes de l’application moment. Bull. Soc. Math. France 116(1988), no. 3, 315–339.Google Scholar
[Do] Dolgachev, I., Lectures on invariant theory. London Mathematical Society Lecture Note Series, 296, Cambridge University Press, Cambridge, 2003.Google Scholar
[DO] Dolgachev, I. and Ortland, D., Point sets in projective spaces and theta functions. Astérisque 165(1988).Google Scholar
[FM] Flaschka, H. and Millson, J., Bending flows for sums of rank one matrices. Canad. J. Math 57(2005), no. 1, 114–158.Google Scholar
[FH] Foth, P. and Hu, Y., Toric degeneration of weight varieties and applications. Trav. Math., XVI, Univ. Luxembourg, 2005, pp. 87–105.Google Scholar
[GGMS] Gel’fand, I. M., Goresky, R. M., MacPherson, R. D., and Serganova, V. V., Combinatorial geometries, convex polyhedra, and Schubert cells. Adv. in Math. 63(1987), no. 3, 301–316. doi:10.1016/0001-8708(87)90059-4Google Scholar
[G] Goldman, W. M., Complex hyperbolic geometry, Oxford Mathematical Monographs, The Clarendon Press, Oxford University Press, New York, 1999.Google Scholar
[GJS] Guillemin, V., Jeffrey, L., and Sjamaar, R., Symplectic implosion. Transform. Groups 7(2002), no. 2, 155–184. doi:10.1007/s00031-002-0009-yGoogle Scholar
[Ha] Harris, J., Algebraic geometry. Graduate Texts in Mathematics, 133, Springer-Verlag, New York, 1995.Google Scholar
[HK] Hausmann, J.-C. and Knutson, A., Polygon spaces and Grassmannians. Enseign. Math. 43(1997), no. 1–2, 173–198.Google Scholar
[HMSV] Howard, B., Millson, J., Snowden, A., and Vakil, R., The equations for the moduli space of n points on the line. Duke Math. J. 146(2009), no. 2, 175–226. doi:10.1215/00127094-2008-063Google Scholar
[Howe] Howe, R., The classical groups and invariants of bilinear forms. In: The mathematical heritage of Hermann Weyl, Proceedings of Symposia in Pure Mathematics, 48, American Mathematical Society, Providence, RI, 1988, pp. 132-166.Google Scholar
[HJ] Hurtubise, J. C. and Jeffrey, L. C., Representations with weighted frames and framed parabolic bundles. Canad. J. Math. 52(2000), no. 6, 1235–1268.Google Scholar
[J] Jeffrey, L. C., Extended moduli spaces of flat connections of flat connections on Riemann surfaces. Math. Ann. 298(1994), no. 4, 667–692. doi:10.1007/BF01459756Google Scholar
[KY] Kamiyama, Y. and Yoshida, T., Symplectic toric space associated to triangle inequalities. Geom. Dedicata 93(2002), 25–36. doi:10.1023/A:1020393910472Google Scholar
[KM] Kapovich, M. and Millson, J. J., The symplectic geometry of polygons in Euclidean space. J. Differential Geom. 44(1996), no. 3, 479–513.Google Scholar
[KN] Kempf, G. and Ness, L., The length of vectors in representation spaces. In: Algebraic geometry (Proc. Summer Meeting, Univ. Copenhagen 1978), Lecture Notes in Math., 732, Springer, Berlin, pp. 233–243.Google Scholar
[Ke] Kempe, A., On regular difference terms. Proc. London Math. Soc. 25(1894), 343–350.Google Scholar
[Kly] Klyachko, A. A., Spatial polygons and stable configurations of points on the projective line. In: Algebraic geometry and its applications (Yaroslavl’, 1992), Aspects Math., E25, Vieweg, Braunschweig, 1994, pp. 67–84.Google Scholar
[KR] Kung, J. P. S. and Rota, G.-C., The invariant theory of binary forms. Bull. Amer. Math. Soc. 10(1984), no. 1, 27–85. doi:10.1090/S0273-0979-1984-15188-7Google Scholar
[LG] Lakshmibai, V. and Gonciulea, N., Flag varieties. Hermann, 2001.Google Scholar
[Mu] Mumford, D., Geometric invariant theory. Ergebnisse der Mathematik und Ihrer Grenzgebiete, 34, Springer-Verlag, Berlin-New York, 1965.Google Scholar
[S] Schwarz, G., The topology of algebraic quotients. In: Topological methods in algebraic transformation groups (New Brunswick, NJ, 1988), Prod. Math., 80, Birkhäuser Boston, Boston, MA, 1989.Google Scholar
[Sh] Shioda, T., On the graded ring of invariants of binary octavics. Amer. J. Math. 89(1967), 1022–1046. doi:10.2307/2373415Google Scholar
[Sj] Sjamaar, R., Holomorphic slices, symplectic reduction and multiplicities of representations. Ann. of Math. 141(1995), no. 1, 87–129. doi:10.2307/2118628Google Scholar
[SjL] Sjamaar, R. and Lerman, E., Stratified symplectic spaces and reduction. Ann. of Math. 134(1991), no. 3, 375–422. doi:10.2307/2944350Google Scholar
[SpSt] Speyer, D. and Sturmfels, B., The tropical Grassmannian. Adv. Geom. 4(2004), no. 3, 389–411. doi:10.1515/advg.2004.023Google Scholar
[St] Sturmfels, B., Gröbner bases and convex polytopes. University Lecture Series, 8, American Mathematical Society, Providence, RI, 1996.Google Scholar