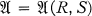Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ryser, H. J.
1960.
Matrices of zeros and ones.
Bulletin of the American Mathematical Society,
Vol. 66,
Issue. 6,
p.
442.
Fulkerson, D. R.
and
Ryser, H. J.
1961.
Widths and Heights of (0,1) -Matrices.
Canadian Journal of Mathematics,
Vol. 13,
Issue. ,
p.
239.
Fulkerson, D. R.
and
Ryser, H. J.
1962.
Multiplicities and Minimal Widths for (0, 1)-Matrices.
Canadian Journal of Mathematics,
Vol. 14,
Issue. ,
p.
498.
Haber, Robert M.
1963.
Minimal Term Rank of a Class of (0, 1)-Matrices.
Canadian Journal of Mathematics,
Vol. 15,
Issue. ,
p.
188.
Fulkerson, D. R.
1964.
The Maximum Number of Disjoint Permutations Contained in a Matrix of Zeros and Ones.
Canadian Journal of Mathematics,
Vol. 16,
Issue. ,
p.
729.
Mesner, Dale M.
1964.
Traces of a Class Of (0, 1)-Matrices.
Canadian Journal of Mathematics,
Vol. 16,
Issue. ,
p.
82.
Brualdi, Richard A.
1980.
Matrices of zeros and ones with fixed row and column sum vectors.
Linear Algebra and its Applications,
Vol. 33,
Issue. ,
p.
159.
Brualdi, Richard A
1980.
Matrices of 0's and 1's with total support.
Journal of Combinatorial Theory, Series A,
Vol. 28,
Issue. 3,
p.
249.
Brualdi, Richard A.
1981.
On Haber's Minimum Term Rank Formula.
European Journal of Combinatorics,
Vol. 2,
Issue. 1,
p.
17.
Anstee, R.P.
1982.
Triangular (0,1)-matrices with prescribed row and column sums.
Discrete Mathematics,
Vol. 40,
Issue. 1,
p.
1.
Anstee, R.P
1985.
An algorithmic proof of Tutte's f-factor theorem.
Journal of Algorithms,
Vol. 6,
Issue. 1,
p.
112.
Ermers, Ruud
and
Polman, Ben
1987.
On the eigenvalues of the structure matrix of matrices of zeros and ones.
Linear Algebra and its Applications,
Vol. 95,
Issue. ,
p.
17.
Nisan, Noam
and
Soroker, Danny
1989.
Parallel Algorithms for Zero-One Supply-Demand Problems.
SIAM Journal on Discrete Mathematics,
Vol. 2,
Issue. 1,
p.
108.
Michael, T.S.
1991.
The structure matrix and a generalization of Ryser's maximum term rank formula.
Linear Algebra and its Applications,
Vol. 145,
Issue. ,
p.
21.
Michael, T.S.
1993.
The structure matrix of the class of r-multigraphs with a prescribed degree sequence.
Linear Algebra and its Applications,
Vol. 183,
Issue. ,
p.
155.
Kuba, Attila
and
Herman, Gabor T.
1999.
Discrete Tomography.
p.
3.
Tsurkov, Vladimir
and
Mironov, Anatoli
1999.
Minimax Under Transportation Constrains.
Vol. 27,
Issue. ,
p.
169.
Tsurkov, Vladimir
and
Mironov, Anatoli
1999.
Minimax Under Transportation Constrains.
Vol. 27,
Issue. ,
p.
123.
Cho, Han Hyuk
Hong, Chan Yong
Kim, Suh-Ryung
Park, Chang Hoon
and
Nam, Yunsun
2001.
On A(R,S) all of whose members are indecomposable.
Linear Algebra and its Applications,
Vol. 332-334,
Issue. ,
p.
119.
Brualdi, Richard A.
and
Dahl, Geir
2003.
Matrices of zeros and ones with given line sums and a zero block.
Linear Algebra and its Applications,
Vol. 371,
Issue. ,
p.
191.