Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T05:40:36.285Z Has data issue: false hasContentIssue false
  • English
  • Français

The Translation Planes of Dempwolff

Published online by Cambridge University Press:  20 November 2018

N. L. Johnson
N. L. Johnson*
Affiliation:
The University of Iowa, Iowa City, Iowa
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [2], Dempwolff constructs three translation planes of order 16 using sharply 2-transitive sets of permutations in S16. That is, if 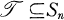acting on Λ is a sharply 2-transitive set of permutations then an affine plane of order n may be defined as follows: The set of points = {(x, y)|x, y ∊ Λ} and the lines = {(x, y)|y = xg for fixed 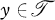}, {(x, y)|x = c}, {(x, y)|y = c} for c ∊ Λ.

Let V be a vector space of dimension k over F ≅ GF(pr). A translation plane may be defined by finding a set M of pkr – 1 linear transformations such that xy–l is fixed point free on 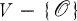for all x ≠ y in M.

Notice that if we allow V to act on itself 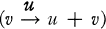then MV is a sharply 2-transitive set on V if and only if xy–1 is fixed point free on 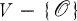for all x ≠ y in M.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 5 , 01 October 1981 , pp. 1060 - 1073
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Dempwolff, V., Eine Klasse Von Translationsebenen uber GF(22k+1). (To appear.)Google Scholar
2. Dempwolff, V., Einige Translationsebenen der Ordnung 16 und Ihre Kollineationen. (To appear.)Google Scholar
3. Foulser, D. A., Johnson, N. L. and Ostrom, T. G., Characterization of the Desarguesian and Hall planes of order q2 by SL(2, q). (To appear.)Google Scholar
4. Jha, V., Finite semi-transitive planes. (To appear.)Google Scholar
5. Johnson, N. L., Translation planes constructed from semi-field planes, Pacific J. Math. 36 (1971), 701–711.Google Scholar
6. Johnson, N. L., Distortion and generalized Hall planes, Geom. Ded. 4 (1975), 437–456.Google Scholar
7. Johnson, N. L., The translation planes of order 16 that admit SL(2, 4). (To appear.)Google Scholar
8. Knuth, D. E., Finite semifields and projective planes, J. Algebra 2 (1965), 182–217.Google Scholar