Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kang, Hyeonbae
and
Koo, Hyungwoon
2000.
Two-weighted inequalities for the derivatives of holomorphic functions and Carleson measures on the unit ball.
Nagoya Mathematical Journal,
Vol. 158,
Issue. ,
p.
107.
Choe, Boo Rim
Koo, Hyungwoon
and
Yi, Heungsu
2004.
Moment vanishing properties of harmonic Bergman functions.
Journal of Mathematical Analysis and Applications,
Vol. 296,
Issue. 2,
p.
365.
Luo, Luo
and
Ueki, Sei-ichiro
2007.
Weighted composition operators between weighted Bergman spaces and Hardy spaces on the unit ball of Cn.
Journal of Mathematical Analysis and Applications,
Vol. 326,
Issue. 1,
p.
88.

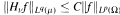 , where
, where 