Unbounded Fredholm Modules and Spectral Flow

Abstract

An odd unbounded (respectively, $p$-summable) Fredholm module for a unital Banach $*$-algebra, 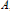$A$, is a pair 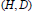$(H,D)$ where 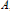$A$ is represented on the Hilbert space, 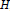$H$, and 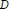$D$ is an unbounded self-adjoint operator on 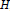$H$ satisfying:

(1) 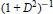${{(1+{{D}^{2}})}^{-1}}$ is compact (respectively, Trace 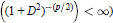$\left( {{\left( 1+{{D}^{2}} \right)}^{-(p/2)}} \right)<\infty $, and

(2) 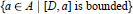$\{a\in A|\,\,[D,a]\,\,\text{is}\,\,\text{bounded}\}\text{ }$ is a dense $*$- subalgebra of 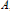$A$.

If $u$ is a unitary in the dense $*$-subalgebra mentioned in (2) then

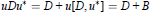$$uD{{u}^{*}}=D+u[D,{{u}^{*}}]=D+B$$

where $B$ is a bounded self-adjoint operator. The path

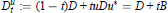$$D_{t}^{u}:=(1-t)D+tuD{{u}^{*}}=D+tB$$

is a “continuous” path of unbounded self-adjoint “Fredholm” operators. More precisely, we show that

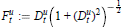$$F_{t}^{u}:=D_{t}^{u}{{\left( 1+{{\left( D_{t}^{u} \right)}^{2}} \right)}^{-\frac{1}{2}}}$$

is a norm-continuous path of (bounded) self-adjoint Fredholm operators. The spectral flow of this path 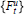$\left\{ F_{t}^{u} \right\}$ (or 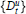$\{D_{t}^{u}\}$) is roughly speaking the net number of eigenvalues that pass through 0 in the positive direction as $t$ runs from 0 to 1. This integer,

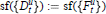$$\text{sf}\left( \left\{ D_{t}^{u} \right\} \right):=\text{sf}\left( \left\{ F_{t}^{u} \right\} \right),$$

recovers the pairing of the 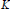$K$-homology class 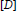$[D]$ with the 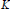$K$-theory class 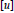$[u]$.

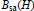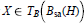We use I.M. Singer's idea (as did E. Getzler in the $\theta $-summable case) to consider the operator $B$ as a parameter in the Banach manifold, ${{B}_{\text{sa}}}\left( H \right)$, so that spectral flow can be exhibited as the integral of a closed 1-form on this manifold. 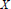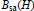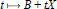Now, for $B$ in our manifold, any $X\,\in \,{{T}_{B}}({{B}_{\text{sa}}}(H))$ is given by an $X$ in ${{B}_{\text{sa}}}(H)$ as the derivative at $B$ along the curve $t\,\mapsto \,B\,+\,tX$ in the manifold. Then we show that for 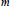$m$ a sufficiently large half-integer:

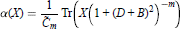$$\alpha (X)=\frac{1}{{{{\tilde{C}}}_{m}}}\text{Tr}\left( X{{\left( 1+{{\left( D+B \right)}^{2}} \right)}^{-m}} \right)$$

is a closed 1-form. For any piecewise smooth path 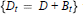$\left\{ {{D}_{t}}=D+{{B}_{t}} \right\}$ with 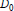${{D}_{0}}$ and 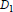${{D}_{1}}$unitarily equivalent we show that

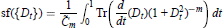$$\text{sf}\left( \left\{ {{D}_{t}} \right\} \right)=\frac{1}{{{{\tilde{C}}}_{m}}}\int_{\text{0}}^{\text{1}}{\text{T}}\text{r}\left( \frac{d}{dt}\left( {{D}_{t}} \right){{\left( 1+D_{1}^{2} \right)}^{-m}} \right)dt$$

the integral of the 1-form $\alpha $. If 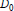${{D}_{0}}$ and 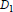${{D}_{1}}$ are not unitarily equivalent, wemust add a pair of correction terms to the right-hand side. We also prove a bounded finitely summable version of the form:

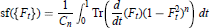$$\text{sf}\left( \left\{ {{F}_{t}} \right\} \right)=\frac{1}{{{C}_{n}}}\int_{\text{0}}^{\text{1}}{\text{T}}\text{r}\left( \frac{d}{dt}\left( {{F}_{t}} \right){{\left( 1-{{F}_{t}}^{2} \right)}^{n}} \right)dt$$

for 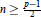$n\ge \frac{p-1}{2}$ an integer. The unbounded case is proved by reducing to the bounded case via the map 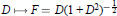$D\mapsto F=D{{(1+{{D}^{2}})}^{-\frac{1}{2}}}$ We prove simultaneously a type II version of our results.