No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 20 November 2018
Let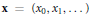 
$\mathbf{x}\,=\,\left( {{x}_{0}},\,{{x}_{1}},.\,.\,. \right)$ be a 
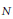$N$-periodic sequence of integers 
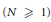$\left( N\,\ge \,1 \right)$, and 
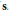$\mathbf{s}$ a sturmian sequence with the same barycenter (and also 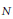$N$-periodic, consequently). It is shown that, for affine functions 
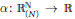$\alpha :\,\mathbb{R}_{(N)}^{\mathbb{N}}\,\to \,\mathbb{R}$ which are increasing relatively to some order 
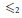${{\le }_{2}}$ on 
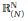$\mathbb{R}_{(N)}^{\mathbb{R}}$ (the space of all 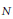$N$-periodic sequences), the average of 
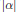$\left| \alpha \right|$ on the orbit of 
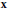$\mathbf{x}$ is greater than its average on the orbit of 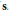$\mathbf{s}$.
Soit 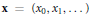$\mathbf{x}\,=\,\left( {{x}_{0}},\,{{x}_{1}},.\,.\,. \right)$ une suite 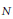$N$-périodique d'entiers 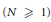$\left( N\,\ge \,1 \right)$, et 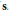$\mathbf{s}$ une suite sturmienne de même barycentre (et donc également 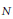$N$-périodique). On montre que, pour les fonctions affines 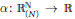$\alpha :\,\mathbb{R}_{(N)}^{\mathbb{N}}\,\to \,\mathbb{R}$ qui sont croissantes relativement à un certain ordre 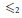${{\le }_{2}}$ sur 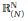$\mathbb{R}_{(N)}^{\mathbb{R}}$ (l'espace de toutes les suites 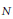$N$-périodiques), la moyenne de 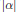$\left| \alpha \right|$ sur l'orbite de 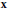$\mathbf{x}$ est plus grande que sa moyenne sur l'orbite de $\mathbf{s}$.
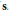You have
Access