No CrossRef data available.
Article contents
Uniform Approximation by Polynomials with Variable Exponents
Published online by Cambridge University Press: 20 November 2018
Extract
We examine questions related to approximating functions by sums of the form
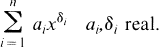
We focus on approximations to functions given by the integral transformation
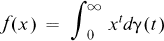
where γ is a positive measure. Approximations to this class of functions (Laplace transforms in the variable — lnx) are particularly well behaved (see Theorem 1). Questions concerning existence, uniqueness and characterization of such approximations have been thoroughly examined in the equivalent setting of exponential sum approximations (see [3], [4], [6] and [9]). Less well studied is the order of convergence of the approximation. This is the problem we address. Part of the motivation for using sums of the form (1), which we shall call Gaussian sums, stems from the observation that all analytic functions with Taylor series expansion having positive coefficients are of the form (2).
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1983


