Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T07:02:17.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform Distribution of Fractional Parts Related to Pseudoprimes

Published online by Cambridge University Press:  20 November 2018

William D. Banks ,
Moubariz Z. Garaev ,
Florian Luca  and
Igor E. Shparlinski
William D. Banks
Affiliation:
Department of Mathematics, University of Missouri, Columbia, MO 65211 USA, bbanks@math.missouri.edu
Moubariz Z. Garaev
Affiliation:
Instituto de Matemáticas, Universidad Nacional Autónoma de México, C.P. 58089, Morelia, Michoacán, México, garaev@matmor.unam.mx, fluca@matmor.unam.mx
Florian Luca
Affiliation:
Instituto de Matemáticas, Universidad Nacional Autónoma de México, C.P. 58089, Morelia, Michoacán, México, garaev@matmor.unam.mx, fluca@matmor.unam.mx
Igor E. Shparlinski
Affiliation:
Department of Computing, Macquarie University, Sydney, NSW 2109, Australia, igor@ics.mq.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We estimate exponential sums with the Fermat-like quotients

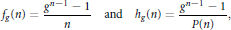$${{f}_{g}}(n)=\frac{{{g}^{n-1}}-1}{n}\text{and }{{h}_{g}}(n)=\frac{{{g}^{n-1}}-1}{P(n)},$$

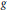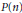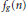where $g$ and $n$ are positive integers, $n$ is composite, and $P\left( n \right)$ is the largest prime factor of $n$. Clearly, both ${{f}_{g}}(n)$ and 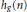${{h}_{g}}(n)$ are integers if $n$ is a Fermat pseudoprime to base 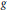$g$, and if $n$ is a Carmichael number, this is true for all 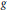$g$ coprime to $n$. Nevertheless, our bounds imply that the fractional parts 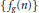$\left\{ {{f}_{g}}(n) \right\}$ and 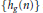$\left\{ {{h}_{g}}(n) \right\}$ are uniformly distributed, on average over 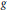$g$ for 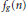${{f}_{g}}(n)$, and individually for 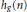${{h}_{g}}(n)$. We also obtain similar results with the functions 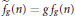${{\tilde{f}}_{g}}(n)=g\,{{f}_{g}}(n)$ and 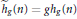${{\tilde{h}}_{g}}(n)=g{{h}_{g}}(n)$.

Keywords

11L0711N3711N60
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 3 , 01 June 2009 , pp. 481 - 502
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Alford, W. R., Granville, A., and Pomerance, C., There are infinitely many Carmichael numbers. Ann. of Math. 139(1994), no. 3, 703–722.Google Scholar
[2] Banks, W. D., Garaev, M. Z., Luca, F., and Shparlinski, I. E., Uniform distribution of the fractional part of the average prime divisor. Forum Math. 17(2005), no. 6, 885–901.Google Scholar
[3] Bassily, N. L., Kátai, I., and Wijsmuller, M., On the prime power divisors of the iterates of the Euler-ϕ function. Publ. Math. Debrece. 55(1999), no. 1-2, 17–32.Google Scholar
[4] Bateman, P. T., Erdös, P., Pomerance, C., and Straus, E. G., The arithmetic mean of the divisors of an integer. In: Analytic number theory, Lecture Notes in Math. 899, Springer, Berlin-New York, 1981, pp. 197–220.Google Scholar
[5] Bourgain, J., New bounds on exponential sums related to Diffie-Hellman distributions. C. R. Math. Acad. Sci. Pari. 338(2004), no. 11, 825–830.Google Scholar
[6] Bourgain, J., Glibichuk, A. A., and Konyagin, S. V., Estimates for the number of sums and products and for exponential sums in fields of prime order. J. London Math. Soc. 73(2006), no. 2, 380–398.Google Scholar
[7] Boyarinov, R. N., Ngongo, I. S., and Chubarikov, V. N., On new metric theorems in the method of A. G. Postnikov. In: IV International conference: modern problems of number theory and its pplications, Current problems III, Mosk. Gos. Univ. im. Lomonosova Mekh.- Mat. Fak., Moscow, 2002, pp. 5–31.Google Scholar
[8] El- Mahassni, E. D., Shparlinski, I. E., and A.Winterhof, Distribution of nonlinear congruential pseudorandom numbers modulo almost squarefree integers. Monatsh. Math. 148(2006), no. 4, 297–307.Google Scholar
[9] Erdös, P., Granville, A., Pomerance, C., and Spiro, C., On the normal behavior of the iterates of some arithmetic functions. In: Analytic number theory, Progr. Math. 85, Birkhäuser, Boston, MA, 1990, pp. 165–204.Google Scholar
[10] Erdʺos, P. and Murty, R., On the order of a (mod p). CR MProc. Lecture Notes 19, American Mathematical Society, Providence, RI, 1999, 87–97.Google Scholar
[11] Erdʺos, P. and Pomerance, C., On the number of false witnesses for a composite number. Math. Comp.46(1986), no. 173, 259–279.Google Scholar
[12] Ford, K., The distribution of integers with a divisorin a given interval. Ann. of Math. 168(2008), no. 2, 367–433.Google Scholar
[13] Garaev, M. Z., The large sieve inequality for the exponential sequence ƛ [O(n15/14+o(1))] modulo primes. Canad. J. Math., 61(2009), 336–350.Google Scholar
[14] Garaev, M. Z., Luca, F., and Shparlinski, I. E., Exponential sums and congruences with factorials. J. Reine Angew. Math. 584(2005), 29–44.Google Scholar
[15] Garaev, M. Z. and Shparlinski, I. E., The large sieve inequality with exponential functions and the distribution of Mersenne numbers modulo primes. Int. Math. Res. Not. 2005(2005), no. 39, 2391–2408.Google Scholar
[16] Granville, A. and Pomerance, C., Two contradictory conjectures concerning Carmichael numbers. Math. Comp. 71(2002), no. 238, 883–908.Google Scholar
[17] Heath-Brown, D. R., An estimate for Heilbronn's exponential sum. In: Analytic number theory 2, Progr. Math. 139, Birkhäuser, Boston, MA, 1996, pp. 451–463.Google Scholar
[18] Heath-Brown, D. R. and Konyagin, S. V., New bounds for Gauss sums derived from kth powers, and for Heilbronn's exponential sum. Q. J. Math. 51(2000), no. 2, 221–235.Google Scholar
[19] Indlekofer, K.-H. and Timofeev, N. M., Divisors of shifted primes. Publ. Math. Debrece. 60(2002), no. 3-4, 307–345.Google Scholar
[20] Karatsuba, A. A., Fractional parts of functions of a special form. Izv. Math. 59(1995), no. 4, 721–740.Google Scholar
[21] Karatsuba, A. A., Analogues of Kloosterman sums. Izv. Math. 59(1995), no. 5, 971–981.Google Scholar
[22] Karatsuba, A. A., Double Kloosterman sums. Math. Note. 66(1999), no. 5-6, 565–569.Google Scholar
[23] Konyagin, S. V., Estimates of trigonometric sums over subgroups and Gauss sums. In: IV International Conference, Modern problems of number theory and its applications, Mosk. Gos. Univ. im. Lomonosova Mekh.- Mat. Fak., Moscow, 2002, pp. 86–114.Google Scholar
[24] Konyagin, S. V. and Shparlinski, I. E., Character sums with exponential functions and their applications. Cambridge Tracts in Mathematics 136, Cambridge University Press, Cambridge, 1999.Google Scholar
[25] Korobov, N. M., Estimates of trigonometric sums and their applications. Uspehi Mat. Nau. 13(1958), no. 4, 185–192.Google Scholar
[26] Korobov, N. M., Double trigonometric sums and their applications to the estimation of rational sums. Mat. Zametk. 6(1969), 25–34.Google Scholar
[27] Landau, E., Über die Zahlentheoretische Function ϕ(n) und ihre Beziehung zum Goldbachschen Satz. Nachr. Königlichen Ges.Wiss. Göttingen, Math.-Phys. Klasse, Göttingen, 1900, 177–186.Google Scholar
[28] Lidl, R. and Niederreiter, H., Finite fields. In: Encyclopedia of mathematics and its applications 20, second edition, Cambridge University Press, Cambridge, 1997.Google Scholar
[29] Luca, F., On f (n) modulo ω(n) and (n) when f is a polynomial. J. Aust. Math. Soc. 77(2004), no. 2, 149–164.Google Scholar
[30] Luca, F. and Pomerance, C., On some problems of Makowski-Schinzel and Erdʺos concerning the arithmetical functions ϕ and σ. Colloq. Math. 92(2002), no. 1, 111–130.Google Scholar
[31] Luca, F. and Sankaranarayanan, A., The distribution of integers n divisible by lω(n). Publ. Inst. Math. 76(90)(2004), 89–99.Google Scholar
[32] Montgomery, H. L., Primes in arithmetic progressions. Michigan Math. J. 17(1970), 33–39.Google Scholar
[33] Montgomery, H. L., Ten lectures on the interface between analytic number theory and harmonic analysis. C MBS Regional Conference Series in Mathematics 84, American Mathematical Society, Providence, RI, 1994.Google Scholar
[34] Montgomery, H. L. and Vaughan, R. C., The large sieve. Mathematika 20(1973), 119–134.Google Scholar
[35] Postnikov, A. G., Ergodic aspects of the theory of congruences and of the theory of Diophantine approximations. Trudy Mat. Inst. Steklo. 82(1966), 3–112.Google Scholar
[36] Prachar, K., Primzahlverteilung. Springer-Verlag, Berlin, 1957.Google Scholar
[37] Spiro, C., How often is the number of divisors of n a divisor of n? J. Number Theor. 21(1985), no. 1, 81–100.Google Scholar
[38] Spiro, C., Divisibility of the k-fold iterated divisor function of n into n. Acta Arith. 68(1994), no. 4, 307–339.Google Scholar
[39] Tenenbaum, G., Introduction to analytic and probabilistic number theory. Studies in Advanced Mathematics 46, Cambridge University Press, 1995.Google Scholar
[40] Vinogradov, A. I., On the remainder in Merten's formula. Dokl. Akad. Nauk SSS. 148(1963), 262–263.Google Scholar
[41] Vinogradov, I. M., Elements of number theory. Dover Publications, New York, 1954.Google Scholar