Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-15T23:27:40.801Z Has data issue: false hasContentIssue false
  • English
  • Français

Unique Extension and Product Measures

Published online by Cambridge University Press:  20 November 2018

Norman Y. Luther
Norman Y. Luther*
Affiliation:
Washington State University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Following (2) we say that a measure μ on a ring 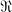is semifinite if

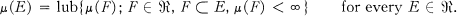
Clearly every σ-finite measure is semifinite, but the converse fails.

In § 1 we present several reformulations of semifiniteness (Theorem 2), and characterize those semifinite measures μ on a ring 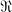that possess unique extensions to the σ-ring generated by 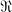(Theorem 3). Theorem 3 extends a classical result for σ-finite measures (3, 13.A). Then, in § 2, we apply the results of § 1 to the study of product measures; in the process, we compare the “semifinite product measure” (1; 2, pp. 127ff.) with the product measure described in (4, pp. 229ff.), finding necessary and sufficient conditions for their equality; see Theorem 6 and, in relation to it, Theorem 7.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 19 , 1967 , pp. 757 - 763
Copyright
Copyright © Canadian Mathematical Society 1967

References

1. Berberian, S. K., The product of two measures, Amer. Math. Monthly, 69 (1962), 961–968.Google Scholar
2. Berberian, S. K., Measure and integration (New York, 1965).Google Scholar
3. Halmos, P. R., Measure theory (New York, 1950).Google Scholar
4. Royden, H. L., Real analysis (New York, 1963).Google Scholar