Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-15T10:33:34.024Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniqueness Theorems for a Singular Partial Differential Equation

Published online by Cambridge University Press:  20 November 2018

P. Ramankutty
P. Ramankutty*
Affiliation:
University of Auckland, Auckland, New Zealand
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A singular partial differential equation which occurs frequently in mathematical physics is given by

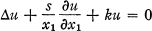
where 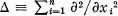is the Laplacian operator on Rn of which the generic point is denoted by x = (x1, … , xn) and s and k are real numbers. The study of solutions of this equation for the case k = 0 was initiated by A. Weinstein [5], who named it ‘Generalized Axially Symmetric Potential Theory'. Numerous references to the literature on this equation can be found in [1; 3; 6]. The analytic theory of equations of the type mentioned above has extensively been treated in [2].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 25 , Issue 1 , February 1973 , pp. 156 - 163
Copyright
Copyright © Canadian Mathematical Society 1973

References

1. Colton, D. and Gilbert, R. P., A contribution to the Vekua-Rellich theory of metaharmonic functions, Amer. J. Math. 92 (1970), 525–540.Google Scholar
2. Gilbert, R. P., Function theoretic methods in the theory of partial differential equations (Academic Press, New York, 1969).Google Scholar
3. Gilbert, R. P., An investigation of the analytic properties of solutions to the generalized axially symmetric, reduced wave equation in n + 1 variables, with an application to the theory of potential scattering, SIAM J. Appl. Math. 16 (1968), 30–50.Google Scholar
4. Hopf, E., ElementareBemerkungenüber die LosungenpartiellerDifferentialgleichungen ZweiterOrdnungvomelliptichenTypus, S.-B.Preuss.Akad.Wiss. 19 (1927), 147–152.Google Scholar
5. Weinstein, A., Generalized axially symmetric potential theory, Bull. Amer. Math. Soc. 59 (1953), 20–38.Google Scholar
6. Weinstein, A., Singular partial differential equations and their applications, Proceedings of the symposium on fluid dynamics and applied mathematics, University of Maryland, 1961 (Gordon and Breach, New York, 29–49).Google Scholar