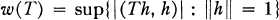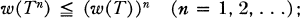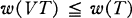Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bhatia, Rajendra
and
Holbrook, John A.R.
1987.
Unitary invariance and spectral variation.
Linear Algebra and its Applications,
Vol. 95,
Issue. ,
p.
43.
Li, Chi-Kwong
and
Tsing, Nam Kiu
1989.
Norms that are invariant under unitary similarities and theC-numerical radii.
Linear and Multilinear Algebra,
Vol. 24,
Issue. 3,
p.
209.
Li, Chi-Kwong
and
Tsing, Nam Kiu
1990.
Linear operators preserving unitary similarity invariant norms.
Linear and Multilinear Algebra,
Vol. 27,
Issue. 3,
p.
213.
Li, Chi-Kwong
1994.
Some aspects of the theory of norms.
Linear Algebra and its Applications,
Vol. 212-213,
Issue. ,
p.
71.
Ando, T.
and
Okubo, K.
1997.
Höder–type inequalities associated with operator radii and schur products†.
Linear and Multilinear Algebra,
Vol. 43,
Issue. 1-3,
p.
53.
Suen, Ching-Yun
1998.
WA Contractions.
Positivity,
Vol. 2,
Issue. 4,
p.
301.
Ando, T.
2001.
Recent Advances in Operator Theory and Related Topics.
p.
29.
Badea, C.
and
Cassier, G.
2002.
Constrained von Neumann Inequalities.
Advances in Mathematics,
Vol. 166,
Issue. 2,
p.
260.
Okubo, K.
and
Woerdeman, H.J.
2002.
Rank Reducing Matrix Norms.
Linear and Multilinear Algebra,
Vol. 50,
Issue. 2,
p.
185.
Kalyuzhnyi-Verbovetzkii, Dmitry S.
2005.
Recent Advances in Operator Theory and its Applications.
p.
273.
Hirzallah, Omar
Kittaneh, Fuad
and
Shebrawi, Khalid
2011.
Numerical Radius Inequalities for Commutators of Hilbert Space Operators.
Numerical Functional Analysis and Optimization,
Vol. 32,
Issue. 7,
p.
739.
Dragomir, Silvestru Sever
2013.
Inequalities for the Numerical Radius of Linear Operators in Hilbert Spaces.
p.
1.
Al-Dolat, Mohammed
Al-Zoubi, Khaldoun
Ali, Mohammed
and
Bani-Ahmad, Feras
2016.
General numerical radius inequalities for matrices of operators.
Open Mathematics,
Vol. 14,
Issue. 1,
p.
109.
Dragomir, Silvestru Sever
2017.
Progress in Approximation Theory and Applicable Complex Analysis.
Vol. 117,
Issue. ,
p.
163.
Gau, Hwa-Long
and
Wang, Kuo-Zhong
2017.
Extremality of numerical radii of matrix commutators and Jordan products.
Linear Algebra and its Applications,
Vol. 533,
Issue. ,
p.
258.
Bhunia, Pintu
Bag, Santanu
and
Paul, Kallol
2019.
Numerical radius inequalities and its applications in estimation of zeros of polynomials.
Linear Algebra and its Applications,
Vol. 573,
Issue. ,
p.
166.
Najafi, H.
2020.
Some numerical radius inequality for several operators.
Linear Algebra and its Applications,
Vol. 588,
Issue. ,
p.
489.
Al-Dolat, Mohammed
Jaradat, Imad
and
Baleanu, Dumitru
2020.
An extension of several essential numerical radius inequalities of $2\times 2$ off-diagonal operator matrices.
Advances in Difference Equations,
Vol. 2020,
Issue. 1,
Bhunia, Pintu
and
Paul, Kallol
2021.
Development of inequalities and characterization of equality conditions for the numerical radius.
Linear Algebra and its Applications,
Vol. 630,
Issue. ,
p.
306.
Bhunia, Pintu
Bag, Santanu
and
Paul, Kallol
2021.
Numerical radius inequalities of operator matrices with applications.
Linear and Multilinear Algebra,
Vol. 69,
Issue. 9,
p.
1635.