Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T09:40:47.505Z Has data issue: false hasContentIssue false
  • English
  • Français

Univalent and Starlike Generalized Hypergeometric Functions

Published online by Cambridge University Press:  20 November 2018

Shigeyoshi Owa  and
H. M. Srivastava
Shigeyoshi Owa
Affiliation:
Kinki University, Osaka, Japan
H. M. Srivastava
Affiliation:
University of Victoria, Victoria, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

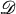A single-valued function f(z) is said to be univalent in a domain if it never takes on the same value twice, that is, if f(z1) = f(z2) for 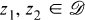implies that z1 = z2. A set 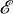is said to be starlike with respect to 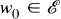the line segment joining w0 to every other point 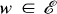lies entirely in 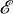. If a function f(z) maps 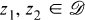onto a domain that is starlike with respect to w0, then f(z) is said to be starlike with respect to w0. In particular, if w0 is the origin, then we say that f(z) is a starlike function. Further, a set 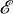is said to be convex if the line segment joining any two points of 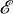lies entirely in 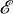. If a function f(z) maps 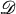onto a convex domain, then we say that f(z) is a convex function in .

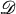Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 5 , 01 October 1987 , pp. 1057 - 1077
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Carlson, B. C. and Shaffer, D. B., Starlike and prestarlike hypergeometric functions, SIAM J. Math. Anal. 75 (1984), 737–745.Google Scholar
2. Duren, P. L., Univalent functions, Grundelheren der Mathematischen Wissenschaften 259 (Springer-Verlag, New York, Berlin, Heidelberg and Tokyo, 1983).Google Scholar
3. Jack, I. S., Functions starlike and convex of order a, J. London Math. Soc. (2) 3 (1971), 469–474.Google Scholar
4. Lewis, J. L., Convexity of a certain series, J. London Math. Soc. (2) 27 (1983), 435–446.Google Scholar
5. MacGregor, T. H., The radius of convexity for starlike functions of order 1/2, Proc. Amer. Math. Soc. 74(1963), 71–76.Google Scholar
6. Merkes, E. P. and Scott, W. T., Starlike hyper geometric functions, Proc. Amer. Math. Soc. 72 (1961), 885–888.Google Scholar
7. Owa, S., On the distortion theorems, I, Kyungpook Math. J. 18 (1978), 53–59.Google Scholar
8. Pinchuk, B., On starlike and convex functions of order α, Duke Math. J. 35 (1968), 721–734.Google Scholar
9. Robertson, M.S., On the theory of univalent functions, Ann. of Math. 37 (1936), 374–408.Google Scholar
10. Ross, B., A brief history and exposition of the fundamental theory of fractional calculus, in Fractional calculus and its applications, (Springer-Verlag, Berlin, Heidelberg and New York, 1975), 1–36.Google Scholar
11. Ruscheweyh, S., Linear operators between classes of prestarlike functions, Comment. Math. Helv. 52 (1977), 497–509.Google Scholar
12. Ruscheweyh, S. and Sheil-Small, T., Hadamard products of schlicht functions and the Pólya-Schoenberg conjecture, Comment. Math. Helv. 48 (1973), 119–135.Google Scholar
13. Schild, A., On starlike functions of order α, Amer. J. Math. 87 (1965), 65–70.Google Scholar
14. Singh, V., Bounds on the curvature of level lines under certain classes of univalent and locally univalent mappings, Indian J. Pure Appl. Math. 10 (1979), 129–144.Google Scholar
15. Srivastava, H. M. and Owa, S., An application of the fractional derivative, Math. Japon. 29 (1984), 383–389.Google Scholar
16. Srivastava, H. M., Owa, S. and Nishimoto, K., Some fractional differintegral equations, J. Math. Anal. Appl. 106 (1985), 360–366.Google Scholar
17. Suffridge, T. J., Starlike functions as limits of polynomials, in Advances in complex function theory, (Springer-Verlag, Berlin, Heidelberg and New York, 1976), 164–203.CrossRefGoogle Scholar
18. Twomey, J. B., On starlike functions, Proc. Amer. Math. Soc. 24 (1970), 95–97.Google Scholar