Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Goodman, A. W.
1968.
Open problems on univalent and multivalent functions.
Bulletin of the American Mathematical Society,
Vol. 74,
Issue. 6,
p.
1035.
Zalcman, Lawrence
1968.
Hadamard products of schlicht functions.
Proceedings of the American Mathematical Society,
Vol. 19,
Issue. 3,
p.
544.
Goodman, A. W.
1969.
The valence of certain means.
Journal d'Analyse Mathématique,
Vol. 22,
Issue. 1,
p.
355.
Shah, S. M.
1972.
Analytic functions with univalent derivatives and entire functions of exponential type.
Bulletin of the American Mathematical Society,
Vol. 78,
Issue. 2,
p.
154.
Shah, S. M.
1977.
Complex Analysis.
Vol. 599,
Issue. ,
p.
117.
Duren, Peter L.
1977.
Coefficients of univalent functions.
Bulletin of the American Mathematical Society,
Vol. 83,
Issue. 5,
p.
891.
MacGregor, T. H.
1985.
Linear Methods in Geometric Function Theory.
The American Mathematical Monthly,
Vol. 92,
Issue. 6,
p.
392.
Ji, Zhou
and
Pingan, Xiao
1993.
A note on the valence of certain means.
Israel Journal of Mathematics,
Vol. 83,
Issue. 3,
p.
289.


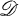 if it is regular in
if it is regular in