Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T02:13:53.700Z Has data issue: false hasContentIssue false
  • English
  • Français

Varieties Obeying Homotopy Laws

Published online by Cambridge University Press:  20 November 2018

Walter Taylor
Walter Taylor*
Affiliation:
University of Colorado, Boulder, Colorado
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

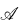The algebraic structure of a topological algebra influences its topological structure in a way which is profound but not well understood. (See § 7 below for various examples.) Here we examine this influence rather generally, and give a fairly complete analysis of one of the many forms it can take, namely, the influence of the identities of 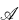on the group identities obeyed by the homotopy group (or groups of the components) of .

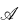Type
Research Article
Information
Canadian Journal of Mathematics , Volume 29 , Issue 3 , 01 June 1977 , pp. 498 - 527
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Adams, J. F., On the non-existence of elements of Hopf invariant one, Ann. Math. (2) 72 (1960), 20–104.Google Scholar
2. Anderson, L. W. and Ward, L. E., A structure theorem for topological lattices, Proc. Glasgow Math. Assoc. 5 (1961), 1–3.Google Scholar
3. Baldwin, J. T. and Berman, J., A logical approach to Malcev conditions, J. Symbolic Logic (to appear).Google Scholar
4. Browder, W., Torsion in H-spaces, Ann. Math. (2) 74 (1961), 24–51.Google Scholar
5. Brown, D. R., Topological semilattices on the two cell, Pacific J. Math. 15 (1965), 35–46.Google Scholar
6. Bulman-Fleming, S. and Taylor, W., Union-indecomposable varieties, Colloq. Math. 35 (1976), 189–199.Google Scholar
7. Cartan, E., La topologie des espaces représentatifs des groupes de Lie, Enseignement Math. 35 (1936), 177-200. Oeuvres complètes (1) 2, 1307–1330.Google Scholar
8. Choe, T. H., Remarks on topological lattices, Kyungpook Math. J. 9 (1969), 59–62.Google Scholar
9. Clifford, A. H., Connected ordered topological semigroups with idempotent endpoints. I, Trans. Amer. Math. Soc. 88 (1958), 80–98.Google Scholar
10. Cook, H., Continua which admit only the identity mapping into non-degenerate subcontinua, Fund. Math. 60 (1967), 241–249.Google Scholar
11. Day, A., A characterization of modularity for congruence lattices of algebras, Can. Math. Bull. 12 (1969), 167–173.Google Scholar
12. Dyer, E. and Shields, A., Connectivity of topological lattices, Pacific J. Math. 9 (1959), 443–448.Google Scholar
13. Evans, T., Products of points—some simple algebras and their identities, Amer. Math. Monthly 74 (1967), 362–372.Google Scholar
14. Fagin, R., A spectrum hierarchy, Z. Math. Logik Grundlagen Math. 21 (1975), 123–134.Google Scholar
15. Faucett, M. W., Compact semigroups irreducibly connected between two points; Topological semigroups and continua with cut points; Proc. Amer. Math. Soc. 6 (1955), 741-747; 748–756.Google Scholar
16. Fossum, R. M., Griffith, P. A. and Reiten, I., Trivial extensions of Abelian categories, Lecture Notes in Math. vol. 456 (Springer-Verlag, Berlin, 1975).Google Scholar
17. Fraser, G. A. and Horn, A., Congruence relations in direct products, Proc. Amer. Math. Soc. 26 (1970), 390–394.Google Scholar
18. Freyd, P., Abelian categories (Harper and Row, N.Y., 1964).Google Scholar
19. Freyd, P. Algebra-valued functors in general and tensor products in particular, Colloq. Math. 14 (1966), 89–106.Google Scholar
20. Gràtzer, G., Universal algebra (van Nostrand, Princeton, 1968).Google Scholar
21. Hagemann, J. and Mitschke, A., On n-permutable congruences, Algebra Universalis 3 (1973), 8–12.Google Scholar
22. Harper, J. R., Homotopy groups of finite H-spaces, Bull. Amer. Math. Soc. 78 (1972), 532–534.Google Scholar
23. Higgins, P. J., Categories and groupoids (van Nostrand Reinhold, London, 1971).Google Scholar
24. Hilton, P. J. and Wylie, S., Homology theory (Cambridge Univ. Press, 1960).Google Scholar
25. Hofmann, K. H. and Mostert, P. S., Elements of compact semigroups (Chas. E. Merrill, Columbus, 1966).Google Scholar
26. Hu, S.-T., Homotopy theory (Academic Press, N.Y., 1959).Google Scholar
27. Huppert, B., Endliche Gruppen I, Vol. 134 of Grundlehren der Mathematischen Wissenschaften (Springer-Verlag, Berlin, 1967).Google Scholar
28. James, I. M., Multiplication on spheres, I. II, Proc. Amer. Math. Soc. 13 (1957), 192-196 and Trans. Amer. Math. Soc. 84 (1957), 545–558.Google Scholar
29. Jônnson, B., Algebras whose congruence lattices are distributive, Math. Scand. 21 (1967), 110–121.Google Scholar
30. Kaplansky, I., Topological rings, Amer. J. Math. 69 (1947), 153–183.Google Scholar
31. Keesee, J. W., An introduction to algebraic topology (Brooks and Cole, Belmont, 1970).Google Scholar
32. Koch, R. J., Compact connected spaces supporting topological semigroups, Semigroup Forum 1 (1970), 95–102.Google Scholar
33. Koch, R. J. and Wallace, A. D., Admissibility of semigroup structures on continua, Trans. Amer. Math. Soc. 88 (1958), 277–287.Google Scholar
34. Lawson, J. D., Boundaries of monoid manifolds, Notices Amer. Math. Soc. 21 (1974), A-112.Google Scholar
35. Lawson, J. D. and Madison, B., Peripherality in semigroups, Semigroup Forum 1 (1970), 128–142.Google Scholar
36. Lawson, J. D. and Williams, W., Topological semilattices and their underlying spaces, Semigroup Forum 1 (1970), 209–223.Google Scholar
37. Maltsev, A. I., On the general theory of algebraic systems (in Russian), Math. Sbornik (N.S.) 35 (77) (1954), 3-20. English translation: Amer. Math. Soc. Transi. (2) 27 (1963), 125–142.Google Scholar
38. Markov, A. A., On free topological groups, Izv. Akad. Nauk SSSR Ser. Mat. 9 (1945). English translation: Amer. Math. Soc. Transi. (1) 8 (1962), 195–272.Google Scholar
39. Nation, J. B., Varieties whose congruences satisfy certain lattice identities, Algebra Universalis 4 (1974), 78–88.Google Scholar
40. Neumann, W. D., On Malcev conditions, J. Austral. Math. Soc. 17 (1974), 376–384.Google Scholar
41. Padmanabhan, R. and Quackenbush, R. W., Equational theories of algebras with distributive congruences, Proc. Amer. Math. Soc. 41 (1973), 373–377.Google Scholar
42. Pareigis, B., Categories and functors (Academic Press, New York, 1970).Google Scholar
43 Rigatelli, L. T., Suite algèbre a-diagonali, Rend. Mat. (6) 7 (1974), 403–414.Google Scholar
44. Schreier, O., Abstrakte Kontinuierliche Gruppen, Abhand. Math. Sem. Hamburg 4 (1926), 15–32.Google Scholar
45. Swierczkowski, S., Topologies in free algebras, Proc. London Math. Soc. (3) 14 (1964), 566–576.Google Scholar
46. Taylor, W., Characterizing Malcev conditions, Algebra Universalis 3 (1973), 351–397.Google Scholar
47. Taylor, W. Uniformity of congruences, Algebra Universalis 4 (1974), 342–360.Google Scholar
48. Taylor, W. The fine spectrum of a variety, Algebra Universalis 5 (1976), 263–303.Google Scholar
49. Taylor, W. Abstracts 74T-A224, 717-A19, 75T-A150 and 76T-A18, Notices Amer. Math. Soc. 21 (1974), A-529 and A-604, 22 (1975), A-451, and 23 (1976), A-5.Google Scholar
50. Wagner, W., Uber die Grundlagen der projektiven Géométrie und allgemeine Zahlensysteme, Math. Z. 113 (1936-37), 528–567.Google Scholar
51. Waliszewski, W., Categories, groupoids, pseudogroups and analytical structures, Rozprawy Matematyczne 45 (1965).Google Scholar
52. Wallace, A. D., Cohomology, dimension and mobs, Summa Brasil. Mat. 3 (1953), 43–55.Google Scholar