Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bokut’, L. A.
Zhevlakov, K. A.
and
Kuz’min, E. N.
1972.
Algebra and Geometry.
Vol. 12,
Issue. ,
p.
3.
Elek, Gábor
2017.
Infinite dimensional representations of finite dimensional algebras and amenability.
Mathematische Annalen,
Vol. 369,
Issue. 1-2,
p.
397.
Schneider, Friedrich Martin
2024.
Group von Neumann Algebras, Inner Amenability, and Unit Groups of Continuous Rings.
International Mathematics Research Notices,
Vol. 2024,
Issue. 8,
p.
6422.


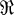 is a regular rank ring, then the rank function can be extended to the matrix ring
is a regular rank ring, then the rank function can be extended to the matrix ring 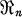 in such a way that
in such a way that 