Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Heinig, H. P.
and
Stepanov, V. D.
1993.
Weighted Hardy Inequalities for Increasing Functions.
Canadian Journal of Mathematics,
Vol. 45,
Issue. 1,
p.
104.
Ostrogorski, Tatyana
1999.
Analysis of Divergence.
p.
309.
Cerdà, Joan
and
Martín, Joaquim
1999.
Interpolation restricted to decreasing functions and Lorentz spaces.
Proceedings of the Edinburgh Mathematical Society,
Vol. 42,
Issue. 2,
p.
243.
Kamińska, Anna
and
Maligranda, Lech
2004.
On Lorentz spaces Γ p,w.
Israel Journal of Mathematics,
Vol. 140,
Issue. 1,
p.
285.
Cerdà, Joan
and
Coll, Heribert
2005.
Function cones and interpolation.
Mathematische Nachrichten,
Vol. 278,
Issue. 3,
p.
227.
Meskhi, A.
2011.
Weighted criteria for the hardy transform under the B p condition in grand lebesgue spaces and some applications.
Journal of Mathematical Sciences,
Vol. 178,
Issue. 6,
p.
622.
Meskhi, Alexander
and
Murtaza, Ghulam
2012.
Potential Operators on Cones of Nonincreasing Functions.
Journal of Function Spaces and Applications,
Vol. 2012,
Issue. ,
p.
1.
Agora, Elona
Carro, María J.
and
Soria, Javier
2012.
Boundedness of the Hilbert transform on weighted Lorentz spaces.
Journal of Mathematical Analysis and Applications,
Vol. 395,
Issue. 1,
p.
218.
Li, HongLiang
2012.
Hardy-type inequalities on strong and weak Orlicz-Lorentz spaces.
Science China Mathematics,
Vol. 55,
Issue. 12,
p.
2493.
Agora, Elona
Carro, María J.
and
Soria, Javier
2013.
Characterization of the Weak-Type Boundedness of the Hilbert Transform on Weighted Lorentz Spaces.
Journal of Fourier Analysis and Applications,
Vol. 19,
Issue. 4,
p.
712.
Miana, Pedro J.
Royo, Juan J.
and
Sánchez-Lajusticia, Luis
2013.
Convolution Algebraic Structures Defined by Hardy-Type Operators.
Journal of Function Spaces and Applications,
Vol. 2013,
Issue. ,
p.
1.
Carro, María J.
and
Domingo-Salazar, Carlos
2016.
Pointwise bounds for integral type operators.
Mathematische Nachrichten,
Vol. 289,
Issue. 11-12,
p.
1386.
Baena-Miret, Sergi
and
Carro, María J.
2021.
Boundedness of Sparse and Rough Operators on Weighted Lorentz Spaces.
Journal of Fourier Analysis and Applications,
Vol. 27,
Issue. 3,
Agora, Elona
Antezana, Jorge
Baena-Miret, Sergi
and
Carro, María J.
2022.
From Weak-type Weighted Inequality to Pointwise Estimate for the Decreasing Rearrangement.
The Journal of Geometric Analysis,
Vol. 32,
Issue. 2,
Baena-Miret, Sergi
and
Carro, María J.
2023.
Weighted estimates for Bochner–Riesz operators on Lorentz spaces.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 153,
Issue. 2,
p.
654.
Singh, Arun Pal
Singh, Monika
Jain, Pankaj
and
Panchal, Rahul
2024.
Rubio de Francia extrapolation theorem in variable Lebesgue spaces for $$B_{p(\cdot )}$$ weights.
Ricerche di Matematica,
Vol. 73,
Issue. 2,
p.
1065.
Baena-Miret, Sergi
2024.
Weighted Strong-Type Estimates on Classical Lorentz Spaces.
The Journal of Geometric Analysis,
Vol. 34,
Issue. 3,


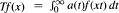 maps the nonnegative nonincreasing functions in
maps the nonnegative nonincreasing functions in 