Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
2005.
Mathematical Inequalities.
Vol. 67,
Issue. ,
p.
485.
2005.
Mathematical Inequalities.
Vol. 67,
Issue. ,
p.
565.
Burenkov, V. I.
Guliev, V. S.
and
Guliev, G. V.
2006.
Necessary and sufficient conditions for the boundedness of the fractional maximal operator in local Morrey-type spaces.
Doklady Mathematics,
Vol. 74,
Issue. 1,
p.
540.
Burenkov, Viktor I.
Guliyev, Huseyn V.
and
Guliyev, Vagif S.
2007.
Necessary and sufficient conditions for the boundedness of fractional maximal operators in local Morrey-type spaces.
Journal of Computational and Applied Mathematics,
Vol. 208,
Issue. 1,
p.
280.
Burenkov, V. I.
Guliev, V. S.
and
Guliev, G. V.
2007.
Necessary and sufficient conditions for the boundedness of the Riesz potential in local Morrey-type spaces.
Doklady Mathematics,
Vol. 75,
Issue. 1,
p.
103.
Gogatishvili, Amiran
Neves, Júlio S.
and
Opic, Bohumír
2009.
Optimal embeddings and compact embeddings of Bessel-potential-type spaces.
Mathematische Zeitschrift,
Vol. 262,
Issue. 3,
p.
645.
Gogatishvili, Amiran
Neves, Júlio S.
and
Opic, Bohumír
2010.
Optimal Embeddings of Bessel-Potential-Type Spaces into Generalized Hölder Spaces Involving k-Modulus of Smoothness.
Potential Analysis,
Vol. 32,
Issue. 3,
p.
201.
Stepanov, Vladimir D.
and
Tikhonov, Sergey Yu.
2011.
Two power-weight inequalities for the Hilbert transform on the cones of monotone functions.
Complex Variables and Elliptic Equations,
Vol. 56,
Issue. 10-11,
p.
1039.
Moura, Susana D.
Neves, Júlio S.
and
Schneider, Cornelia
2011.
Optimal Embeddings of Spaces of Generalized Smoothness in the Critical Case.
Journal of Fourier Analysis and Applications,
Vol. 17,
Issue. 5,
p.
777.
Gogatishvili, Amiran
and
Stepanov, Vladimir D.
2013.
Reduction theorems for operators on the cones of monotone functions.
Journal of Mathematical Analysis and Applications,
Vol. 405,
Issue. 1,
p.
156.
Chen, Jianqing
and
Rocha, Eugénio M.
2013.
Advances in Harmonic Analysis and Operator Theory.
p.
123.
Arendarenko, L. S.
Oinarov, R.
and
Persson, L.-E.
2013.
Advances in Harmonic Analysis and Operator Theory.
p.
77.
Гогатишвили, Амиран
Gogatishvili, Amiran
Степанов, Владимир Дмитриевич
and
Stepanov, Vladimir Dmitrievich
2013.
Редукционные теоремы для весовых интегральных неравенств на конусе монотонных функций.
Успехи математических наук,
Vol. 68,
Issue. 4(412),
p.
3.
Gogatishvili, A
and
Stepanov, V D
2013.
Reduction theorems for weighted integral inequalities on the cone of monotone functions.
Russian Mathematical Surveys,
Vol. 68,
Issue. 4,
p.
597.
Moura, Susana D.
Neves, Júlio S.
and
Schneider, Cornelia
2014.
Spaces of generalized smoothness in the critical case: Optimal embeddings, continuity envelopes and approximation numbers.
Journal of Approximation Theory,
Vol. 187,
Issue. ,
p.
82.
Stepanov, V. D.
and
Shambilova, G. E.
2017.
On bilinear weighted inequalities on the cone of nondecreasing functions.
Doklady Mathematics,
Vol. 96,
Issue. 3,
p.
631.
Степанов, В.Д.
and
Шамбилова, Г.Э.
2017.
О БИЛИНЕЙНЫХ ВЕСОВЫХ НЕРАВЕНСТВАХ НА КОНУСЕ НЕУБЫВАЮЩИХ ФУНКЦИЙ, "Доклады Академии наук".
Доклады Академии Наук,
p.
652.
Stepanov, V. D.
and
Shambilova, G. E.
2018.
Reduction of Weighted Bilinear Inequalities with Integration Operators on the Cone of Nondecreasing Functions.
Siberian Mathematical Journal,
Vol. 59,
Issue. 3,
p.
505.
Neves, Júlio S.
and
Opic, Bohumír
2020.
Optimal local embeddings of Besov spaces involving only slowly varying smoothness.
Journal of Approximation Theory,
Vol. 254,
Issue. ,
p.
105393.
Lai, Baofeng
and
Wang, Runqiu
2021.
On the Best Constant Problem for a Class of Mixed-Norm Hardy Inequalities.
Acta Applicandae Mathematicae,
Vol. 172,
Issue. 1,

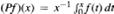 , with non-decreasing function ƒ, is bounded between various weighted
, with non-decreasing function ƒ, is bounded between various weighted 