Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T17:09:47.832Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted Inequalities for Hardy–Steklov Operators

Published online by Cambridge University Press:  20 November 2018

A. L. Bernardis ,
F. J. Martín-Reyes  and
P. Ortega Salvador
A. L. Bernardis
Affiliation:
IMAL-CONICET, Güemes 3450, (3000) Santa Fe, Argentina email: bernard@ceride.gov.ar
F. J. Martín-Reyes
Affiliation:
Análisis Matemático, Facultad de Ciencias, Universidad de Málaga, 29071 Málaga, Spain email: martin_reyes@uma.es, ortega@anamat.cie.uma.es
P. Ortega Salvador
Affiliation:
Análisis Matemático, Facultad de Ciencias, Universidad de Málaga, 29071 Málaga, Spain email: martin_reyes@uma.es, ortega@anamat.cie.uma.es
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We characterize the pairs of weights 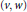$\left( v,\,w \right)$ for which the operator 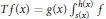$Tf\left( x \right)=g\left( x \right)\int{_{s\left( x \right)}^{h\left( x \right)}}\,f\,$ with $s$ and 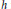$h$ increasing and continuous functions is of strong type 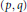$\left( p,\,q \right)$ or weak type 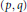$\left( p,\,q \right)$ with respect to the pair 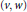$\left( v,\,w \right)$ in the case 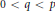$0\,<\,q\,<\,p$ and 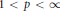$1\,<\,p\,<\,\infty$. The result for the weak type is new while the characterizations for the strong type improve the ones given by H. P. Heinig and G. Sinnamon. In particular, we do not assume differentiability properties on $s$ and 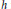$h$ and we obtain that the strong type inequality 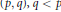$\left( p,q \right),q\,<p$, is characterized by the fact that the function

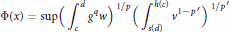$$\Phi \left( x \right)\,=\,\sup \,{{\left( \int_{c}^{d}{{{g}^{q}}w} \right)}^{1/p}}\left( \int_{s\left( d \right)}^{h\left( c \right)}{{{v}^{1-{p}'}}} \right){{\,}^{1/{p}'}}$$

belongs to 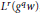${{L}^{r}}\left( {{g}^{q}}w \right)$, where 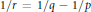${1}/{r\,=\,{\,1}/{q\,-\,{1}/{p}\;}\;}\;$ and the supremum is taken over all $c$ and $d$ such that 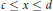$c\le x\le d$ and 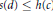$s\left( d \right)\,\le \,h\left( c \right)$.

Keywords

26D1546E3042B25Hardy–Steklov operatorweightsinequalities
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 2 , 01 April 2007 , pp. 276 - 295
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Bernardis, A. L., Martín-Reyes, F. J. and Ortega Salvador, P., A new proof of the characterization of the weighted Hardy inequality. Proc. Roy. Soc. Edinburgh Sect. A 135(2005), no. 5, 941–945.Google Scholar
[2] Chen, T. and Sinnamon, G., Generalized Hardy operators and normalizing measures. J. Inequal. Appl. 7(2002), no. 6, 829–866.Google Scholar
[3] Gogatishvili, A. and Lang, J., The generalized Hardy operator with kernel and variable integral limits in Banach function spaces. J. Inequal. Appl. 4(1999), no. 1, 1–16.Google Scholar
[4] Heinig, H. P. and Sinnamon, G., Mapping properties of integral averaging operators. Studia Math. 129(1998), no. 2, 157–177.Google Scholar
[5] Kufner, A. and Persson, L. E., Weighted Inequalities of Hardy type. World Scientific, Riveredge, NJ, 2003.Google Scholar
[6] Lai, Q., Weighted modular inequalities for Hardy type operators. Proc. London Math. Soc. 79(1999), 649–672 Google Scholar
[7] Martín-Reyes, F. J. and Ortega, P., On weighted weak type inequalities for modified Hardy operators. Proc. Amer. Math. Soc. 126(1998), no. 6, 1739–1746.Google Scholar
[8] Maz’ja, W. G., Sobolev Spaces. Springer-Verlag, Berlin, 1985.Google Scholar
[9] Sawyer, E., Weighted Lebesgue and Lorentz norm inequalities for the Hardy operator. Trans. Amer. Math. Soc. 281(1984), no. 1, 329–337.Google Scholar