Hostname: page-component-7f64f4797f-n5rmq Total loading time: 0 Render date: 2025-11-04T13:29:59.704Z Has data issue: false hasContentIssue false
  • English
  • Français

Weighted Interpolation Inequalities and Embeddings in Rn

Published online by Cambridge University Press:  20 November 2018

R. C. Brown  and
D. B. Hinton
R. C. Brown
Affiliation:
Department of Mathematics, University of Alabama, Tuscaloosa, AL 35487-0350
D. B. Hinton
Affiliation:
Department of Mathematics, University of Tennessee, Knoxville, TN 37996-1300
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

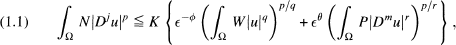This paper is a continuation of [3] which initiated a systematic study of sufficient conditions for the weighted interpolation inequality of sum form, 1.1 to hold. Here ϕ, θ are non-negative functions of m, j, p, q, r, Ω is a bounded or unbounded domain in Rn, ∊ belongs to an interval Γ=(0, ∊ 0), u is in a certain Banach space E(Ω), and N, W, P are measurable real functions satisfying N≧ 0, W, P > 0, as well as additional conditions stated below. Finally the constant K does not depend on u although it may depend on the other parameters.

Keywords

26D1026D2054C25

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 42 , Issue 6 , 01 December 1990 , pp. 959 - 980
Copyright
Copyright © Canadian Mathematical Society 1990

References

1. Adams, R.A., “Sobolev Spaces,” Academic Press, New York, 1975.Google Scholar
2. Brown, R.C. and Hinton, D.B., Necessary and sufficient conditions for one variable weighted interpolation inequalities, J. London Math. Soc. (2)35 (1987), 439–453.Google Scholar
3. Brown, R.C. and Hinton, D.B., Weighted interpolation inequalities of sum and product form in Rn , Proc. London Math. Soc. (3)56(1988), 261–280.Google Scholar
4. Edmunds, D.E. and Evans, W.D., “Spectral Theory and Differential Operators,” Oxford University Press, 1987.Google Scholar
5. Evans, W.D., Kwong, N.K., and Zettl, A., Lower bounds for the spectrum of ordinary differential operators, J. Differential Eqs. 48(1983), 123-155.CrossRefGoogle Scholar
6. Garcia-Cuerva, J. and Rubio De Francia, J., “Weighted norm inequalities and related topics,“ North Holland, Amsterdam, 1985.Google Scholar
7. Gurka, P. and Opic, B., Continuous and compact imbeddings of weighted Sobolev spaces I, Czech. Math. J. 38(1988), 611–617.Google Scholar
8. Gurka, P. and Opic, B., Continuous and compact imbeddings of weighted Sobolev spaces II, Czech. Math. J. 39 (1989), 78–94.Google Scholar
9. Gurka, P. and Opic, B., N-dimensional Hardy inequality and imbedding theorems for weightedSobolev spaces on unbounded domains. To appear in Proceedings, Summer School on Function Spaces, etc., Sodankyla, Finland.Google Scholar
10. Gutierrz, C.E. and Wheeden, R.L., Interpolation inequalities with weights, to appear.Google Scholar
11. Guzmann, Miguel De, Differentiation of Integrals in Rn , in “Lecture Notes in Mathematics 481,“ Springer, Berlin, 1975.CrossRefGoogle Scholar
12. Kufner, A., “Weighted Sobolev Spaces,” John Wiley and Sons, Chichester, 1985.Google Scholar
13. Kufner, A., John, O., and Fucik, S., “Function Spaces,” Noordhoff International Publishing, Leyden, 1977.Google Scholar
14. Kwong, M.K. and Zettl, A., Ramifications of Landau's inequality, Proc. Roy. Soc. Edinburgh A86(1980), 175-212.Google Scholar
15. Kwong, M.K. and Zettl, A., Weighted norm inequalities of sum form involving derivatives, Proc. Roy. Soc. Edinburgh A88(1981), 121-134.Google Scholar
16. Lin, C.S., Interpolation inequalities with weights, Comm. Partial Differential Eqs. 11(1986), 1515–1538.Google Scholar
17. Opic, B., Necessary and sufficient conditions for imbedding in weighted Sobolev spaces, Càsopis pro pěst Math. 114(1989), 165–175.Google Scholar
18. Triebel, H., “Interpolation Theory, Function Spaces, Differential Operators,” North Holland, Amsterdam, 1978.Google Scholar