Article contents
The Word Problem for Orthogroups
Published online by Cambridge University Press: 20 November 2018
Extract
A semigroup which is a union of groups is said to be completely regular. If in addition the idempotents form a subsemigroup, the semigroup is said to be orthodox and is called an orthogroup. A completely regular semigroup S is provided in a natural way with a unary operation of inverse by letting a-l for a ∈ S be the group inverse of a in the maximal subgroup of S to which a belongs. This unary operation satisfies the identities
(1)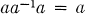
(2)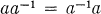
(3)
In fact a completely regular semigroup can be defined as a unary semigroup (a semigroup with an added unary operation) satisfying these identities. An orthogroup can be characterized as a completely regular semigroup satisfying the additional identity
(4)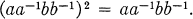
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1981
References
- 7
- Cited by


