No CrossRef data available.
Published online by Cambridge University Press: 08 January 2025
In this paper, we first introduce the concept of symmetric biderivation radicals and characteristic subalgebras of Lie algebras and study their properties. Based on these results, we precisely determine biderivations of some Lie algebras including finite-dimensional simple Lie algebras over arbitrary fields of characteristic not 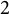 $2$ or
$2$ or  $3$, and the Witt algebras
$3$, and the Witt algebras  $\mathcal {W}^+_n$ over fields of characteristic
$\mathcal {W}^+_n$ over fields of characteristic  $0$. As an application, commutative post-Lie algebra structure on the aforementioned Lie algebras is shown to be trivial.
$0$. As an application, commutative post-Lie algebra structure on the aforementioned Lie algebras is shown to be trivial.
This work is supported by the National Natural Science Foundation of China (Grant Nos. 12271345 and 12071136) and NSERC (311907-2020).