Article contents
Bohr–Rogosinski radius for a certain class of close-to-convex harmonic mappings
Published online by Cambridge University Press: 31 January 2023
Abstract
Let 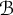 $ \mathcal {B} $ be the class of analytic functions
$ \mathcal {B} $ be the class of analytic functions 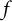 $ f $ in the unit disk
$ f $ in the unit disk 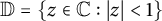 $ \mathbb {D}=\{z\in \mathbb {C} : |z|<1\} $ such that
$ \mathbb {D}=\{z\in \mathbb {C} : |z|<1\} $ such that 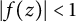 $ |f(z)|<1 $ for all
$ |f(z)|<1 $ for all 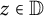 $ z\in \mathbb {D} $. If
$ z\in \mathbb {D} $. If 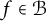 $ f\in \mathcal {B} $ of the form
$ f\in \mathcal {B} $ of the form 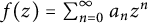 $ f(z)=\sum _{n=0}^{\infty }a_nz^n $, then
$ f(z)=\sum _{n=0}^{\infty }a_nz^n $, then 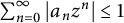 $ \sum _{n=0}^{\infty }|a_nz^n|\leq 1 $ for
$ \sum _{n=0}^{\infty }|a_nz^n|\leq 1 $ for 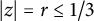 $ |z|=r\leq 1/3 $ and
$ |z|=r\leq 1/3 $ and 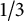 $ 1/3 $ cannot be improved. This inequality is called Bohr inequality and the quantity
$ 1/3 $ cannot be improved. This inequality is called Bohr inequality and the quantity 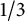 $ 1/3 $ is called Bohr radius. If
$ 1/3 $ is called Bohr radius. If 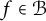 $ f\in \mathcal {B} $ of the form
$ f\in \mathcal {B} $ of the form 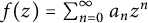 $ f(z)=\sum _{n=0}^{\infty }a_nz^n $, then
$ f(z)=\sum _{n=0}^{\infty }a_nz^n $, then 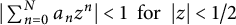 $ |\sum _{n=0}^{N}a_nz^n|<1\;\; \mbox {for}\;\; |z|<{1}/{2} $ and the radius
$ |\sum _{n=0}^{N}a_nz^n|<1\;\; \mbox {for}\;\; |z|<{1}/{2} $ and the radius 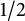 $ 1/2 $ is the best possible for the class
$ 1/2 $ is the best possible for the class 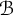 $ \mathcal {B} $. This inequality is called Bohr–Rogosinski inequality and the corresponding radius is called Bohr–Rogosinski radius. Let
$ \mathcal {B} $. This inequality is called Bohr–Rogosinski inequality and the corresponding radius is called Bohr–Rogosinski radius. Let 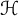 $ \mathcal {H} $ be the class of all complex-valued harmonic functions
$ \mathcal {H} $ be the class of all complex-valued harmonic functions 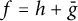 $ f=h+\bar {g} $ defined on the unit disk
$ f=h+\bar {g} $ defined on the unit disk 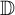 $ \mathbb {D} $, where
$ \mathbb {D} $, where 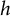 $ h $ and
$ h $ and 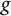 $ g $ are analytic in
$ g $ are analytic in 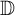 $ \mathbb {D} $ with the normalization
$ \mathbb {D} $ with the normalization 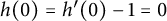 $ h(0)=h^{\prime }(0)-1=0 $ and
$ h(0)=h^{\prime }(0)-1=0 $ and 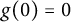 $ g(0)=0 $. Let
$ g(0)=0 $. Let 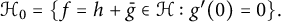 $ \mathcal {H}_0=\{f=h+\bar {g}\in \mathcal {H} : g^{\prime }(0)=0\}. $ For
$ \mathcal {H}_0=\{f=h+\bar {g}\in \mathcal {H} : g^{\prime }(0)=0\}. $ For 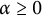 $ \alpha \geq 0 $ and
$ \alpha \geq 0 $ and 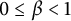 $ 0\leq \beta <1 $, let
$ 0\leq \beta <1 $, let 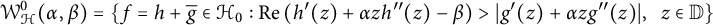 $$ \begin{align*} \mathcal{W}^{0}_{\mathcal{H}}(\alpha, \beta)=\{f=h+\overline{g}\in\mathcal{H}_{0} : \mathrm{Re}\left(h^{\prime}(z)+\alpha zh^{\prime\prime}(z)-\beta\right)>|g^{\prime}(z)+\alpha zg^{\prime\prime}(z)|,\;\; z\in\mathbb{D}\} \end{align*} $$
$$ \begin{align*} \mathcal{W}^{0}_{\mathcal{H}}(\alpha, \beta)=\{f=h+\overline{g}\in\mathcal{H}_{0} : \mathrm{Re}\left(h^{\prime}(z)+\alpha zh^{\prime\prime}(z)-\beta\right)>|g^{\prime}(z)+\alpha zg^{\prime\prime}(z)|,\;\; z\in\mathbb{D}\} \end{align*} $$
be a class of close-to-convex harmonic mappings in 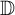 $ \mathbb {D} $. In this paper, we prove the sharp Bohr–Rogosinski radius for the class
$ \mathbb {D} $. In this paper, we prove the sharp Bohr–Rogosinski radius for the class 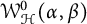 $ \mathcal {W}^{0}_{\mathcal {H}}(\alpha , \beta ) $.
$ \mathcal {W}^{0}_{\mathcal {H}}(\alpha , \beta ) $.
Keywords
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
V.A. is supported by SERB-CRG.
References
- 1
- Cited by


