Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T12:19:10.033Z Has data issue: false hasContentIssue false
  • English
  • Français

Brill-Noether generality of binary curves

Part of: Curves

Published online by Cambridge University Press:  13 October 2020

Xiang He
Xiang He*
Affiliation:
Einstein Institute of Mathematics, Edmond J. Safra Campus, The Hebrew University of Jerusalem, Givat Ram. Jerusalem, 9190401, Israel
*
e-mail:xiang.he@mail.huji.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the space 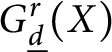$G^r_{\underline d}(X)$ of linear series of certain multi-degree 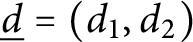$\underline d=(d_1,d_2)$ (including the balanced ones) and rank r on a general genus-g binary curve X has dimension 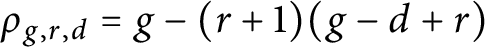$\rho _{g,r,d}=g-(r+1)(g-d+r)$ if nonempty, where 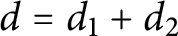$d=d_1+d_2$ . This generalizes Caporaso’s result from the case 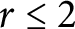$r\leq 2$ to arbitrary rank, and shows that the space of Osserman-limit linear series on a general binary curve has the expected dimension, which was known for 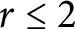$r\leq 2$ . In addition, we show that the space 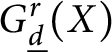$G^r_{\underline d}(X)$ is still of expected dimension after imposing certain ramification conditions with respect to a sequence of increasing effective divisors supported on two general points 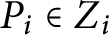$P_i\in Z_i$ , where 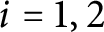$i=1,2$ and 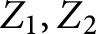$Z_1,Z_2$ are the two components of X. Our result also has potential application to the lifting problem of divisors on graphs to divisors on algebraic curves.

Keywords

Algebraic curveslinear systemsBrill–Noether theory

MSC classification

Primary: 14H10: Families, moduli (algebraic)
Secondary: 14H51: Special divisors (gonality, Brill-Noether theory) 14H60: Vector bundles on curves and their moduli
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 4 , December 2021 , pp. 787 - 807
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altman, A. B. and Kleiman, S. L., Compactifying the picard scheme . Adv. Math. 35(1980), no. 1, 50–112. http://dx.doi.org/10.1016/0001-8708(80)90043-2 CrossRefGoogle Scholar
Amini, O. and Baker, M., Linear series on metrized complexes of algebraic curves . Math. Ann. 362(2015), nos. 1-2, 55–106. http://dx.doi.org/10.1007/s00208-014-1093-8 CrossRefGoogle Scholar
Arbarello, E., Cornalba, M., Griffiths, P., and Harris, J.D., Geometry of algebraic curves. Grundlehren der mathematischen Wissenschaften, v.1, Springer, New York, 2013.Google Scholar
Baker, M. and Jensen, D., Degeneration of linear series from the tropical point of view and applications. In: Nonarchimedean and tropical geometry, Simons Symp., Springer, Cham, 2016, pp. 365–433.Google Scholar
Caporaso, L., Brill-noether theory of binary curves . Math. Res. Lett. 17(2010), no. 2, 243–262.CrossRefGoogle Scholar
Cartwright, D., Jensen, D., and Payne, S., Lifting divisors on a generic chain of loops . Canad. Math. Bull. 58(2015), no. 2, 250–262.CrossRefGoogle Scholar
Cools, F., Draisma, J., Payne, S., and Robeva, E., A tropical proof of the brill–noether theorem . Adv. Math. 230(2012), no. 2, 759–776. http://dx.doi.org/10.1016/j.aim.2012.02.019 CrossRefGoogle Scholar
Eisenbud, D. and Harris, J., Limit linear series: basic theory. Invent. Math. 85(1986), no. 2, 337–371. http://dx.doi.org/10.1007/BF0139094 Google Scholar
Esteves, E., Compactifying the relative Jacobian over families of reduced curves . Trans. Amer. Math. Soc. 353(2001), no. 8, 3045–3095. http://dx.doi.org/10.1090/S0002-9947-01-02746-5 CrossRefGoogle Scholar
Griffiths, P. and Harris, J., On the variety of special linear systems on a general algebraic curve . Duke Math. J. 47(1980), no. 1, 233–272.10.1215/S0012-7094-80-04717-1CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry . Graduate Texts in Mathematics, 52, Springer-Verlag, New York, 1977,CrossRefGoogle Scholar
He, X., Lifting divisors with imposed ramifications on a generic chain of loops . Proc. Amer. Math. Soc. 146(2018), no. 11, 4591–4604. http://dx.doi.org/10.1090/proc/14162 CrossRefGoogle Scholar
He, X., Smoothing of limit linear series on curves and metrized complexes of pseudocompact type . Canad. J. Math. 71(2019), no. 3, 629–658. http://dx.doi.org/10.4153/s0008414x18000068 CrossRefGoogle Scholar
Mumford, D., Fogarty, J., and Kirwan, F., Geometric invariant theory. 3rd ed., Ergebnisse der Mathematik und ihrer Grenzgebiete, 34, Springer-Verlag, 1994. http://dx.doi.org/10.1007/978-3-642-57916-5 CrossRefGoogle Scholar
Oda, T. and Seshadri, C. S., Compactifications of the generalized Jacobian variety . Trans. Amer. Math. Soc. 253(1979), 1–90. http://dx.doi.org/10.2307/1998186 CrossRefGoogle Scholar
Osserman, B., Limit linear series. www.math.ucdavis.edu/osserman/math/llsbook.pdf Google Scholar
Osserman, B., A limit linear series moduli scheme . Ann. Inst. Fourier 56(2006), no. 4, 1165–1205.CrossRefGoogle Scholar
Osserman, B., Dimension counts for limit linear series on curves not of compact type . Math. Z. 284(2016), nos. 1–2, 69–93. http://dx.doi.org/10.1007/s00209-016-1646-5 CrossRefGoogle Scholar
Osserman, B., Limit linear series for curves not of compact type . J. Reine Angew. Math. 753(2019), 57–88. http://dx.doi.org/10.1515/crelle-2017-0003 CrossRefGoogle Scholar