No CrossRef data available.
Article contents
Decidability problem for exponential equations in finitely presented groups
Published online by Cambridge University Press: 22 November 2022
Abstract
We study the following decision problem: given an exponential equation  $a_1g_1^{x_1}a_2g_2^{x_2}\dots a_ng_n^{x_n}=1$ over a recursively presented group G, decide if it has a solution with all
$a_1g_1^{x_1}a_2g_2^{x_2}\dots a_ng_n^{x_n}=1$ over a recursively presented group G, decide if it has a solution with all 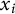 $x_i$ in
$x_i$ in 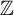 $\mathbb {Z}$. We construct a finitely presented group G where this problem is decidable for equations with one variable and is undecidable for equations with two variables. We also study functions estimating possible solutions of such an equation through the lengths of its coefficients with respect to a given generating set of G. Another result concerns Turing degrees of some natural fragments of the above problem.
$\mathbb {Z}$. We construct a finitely presented group G where this problem is decidable for equations with one variable and is undecidable for equations with two variables. We also study functions estimating possible solutions of such an equation through the lengths of its coefficients with respect to a given generating set of G. Another result concerns Turing degrees of some natural fragments of the above problem.
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
References
Bier, A., and Bogopolski, O., Exponential equations in acylindrically hyperbolic groups. Preprint, 2021. arXiv:2106.11385v1
CrossRefGoogle Scholar
Bilanovic, I., Chubb, J., and Roven, S.,
Detecting properties from presentations of groups
. Arch. Math. Log. 59(2020), 293–312.CrossRefGoogle Scholar
Donald, J.,
Collins, on embedding groups and the conjugacy problem
. J. Lond. Math. Soc. (2) 1(1996), 674–682.Google Scholar
Dudkin, F. and Treyer, A.,
Knapsack problem for Baumslag–Solitar groups
. Siberian J. Pure Appl. Math. 18(2018), no. 4, 43–55.Google Scholar
Figelius, M., Ganardi, M., Lohrey, M., and Zetzsche, G.,
The complexity of knapsack problems in wreath products
. In: Proceedings of the 47th international colloquium on automata, languages, and programming, ICALP 2020, Leibniz International Proceedings in Informatics, 168, Schloss Dagstuhl—Leibniz-Zentrum für Informatik, Germany, 2020, pp. 126:1–126:18.Google Scholar
Frenkel, E., Nikolaev, A., and Ushakov, A.,
Knapsack problems in products of groups
. J. Symb. Comput. 76(2016), 96–108.CrossRefGoogle Scholar
Ganardi, M., König, D., Lohrey, M., and Zetzsche, G.,
Knapsack problems for wreath products
. In: Proceedings of STACS (2018), Leibniz International Proceedings in Informatics, 96, Schloss Dagstuhl—Leibniz-Zentrum für Informatik, Germany, 2018, pp. 1–13.Google Scholar
Kharlampovich, O.,
The word problem for the Burnside varieties
. J. Algebra 173(1995), 613–621.CrossRefGoogle Scholar
König, D., Lohrey, M., and Zetzsche, G.,
Knapsack and subset sum problems for nilpotent, polycyclic, and co-context-free groups
. In: Algebra and computer science, Contemporary Mathematics, 677, American Mathematical Society, Providence, RI, 2016, pp. 138–153.Google Scholar
Lohrey, M.,
Rational subsets of unitriangular groups
. Int. J. Algebra Comput. 25(2015), nos. 1–2, 113–121.CrossRefGoogle Scholar
Lohrey, M.,
Knapsack in hyperbolic groups
. J. Algebra 545(2020), no. 1, 390–415.CrossRefGoogle Scholar
Lohrey, M. and Zetzsche, G.,
Knapsack in graph groups, HNN-extensions and amalgamated products
. Theory Comput. Syst. 62(2018), no. 1, 192–246.CrossRefGoogle Scholar
Lohrey, M. and Zetzsche, G.,
Knapsack and the power word problem in solvable Baumslag–Solitar groups
. In: Proceedings of the 45th international symposium on mathematical foundations of computer science, MFCS 2020, Leibniz International Proceedings in Informatics, 170, Schloss Dagstuhl—Leibniz-Zentrum für Informatik, Germany, 2020, pp. 67:1–67:15.Google Scholar
McCool, J.,
Unsolvable problems in groups with solvable word problem
. Can. J. Math. 22(1970), 836–838.CrossRefGoogle Scholar
Mishchenko, A. and Treier, A.,
Knapsack problem for nilpotent groups
. Groups Complex. Cryptol. 9(2017), no. 1, 87–98.CrossRefGoogle Scholar
Myasnikov, A., Nikolaev, A., and Ushakov, A.,
Knapsack problems in groups
. Math. Comp. 84(2015), no. 292, 987–1016.CrossRefGoogle Scholar
Ol’shanskii, A. Yu.,
SQ-universality of hyperbolic groups
. Mat. Sb. 186(1995), no. 8, 119–132.Google Scholar
Ol’shanskii, A. Y. and Sapir, M. V.,
The conjugacy problem and Higman embeddings
. Mem. Amer. Math. Soc. 170(2004), no. 804, vii + 131.Google Scholar
Ol’shanskii, A. Y. and Sapir, M. V.,
Subgroups of finitely presented groups with solvable conjugacy problem
. Int. J. Algebra Comput. 15(2005), nos. 5–6, 1–10.Google Scholar
Ol’shanskii, A. Yu. and Sapir, M. V., Algorithmic problems in groups with quadratic Dehn function. Preprint, 2020. arXiv:2012.10417v1
Google Scholar


