Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-11T03:53:35.519Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized 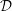${\mathcal{D}}$-Einstein Real Hypersurfaces in 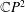$\mathbb{C}P^{2}$ and 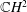$\mathbb{C}H^{2}$

Part of: Local differential geometry Symplectic geometry, contact geometry

Published online by Cambridge University Press:  27 February 2020

Yaning Wang
Yaning Wang*
Affiliation:
School of Mathematics and Information Science, Henan Normal University, Xinxiang453007, Henan, P. R. China Email: wyn051@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we obtain some new characterizations of pseudo-Einstein real hypersurfaces in 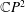$\mathbb{C}P^{2}$ and 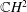$\mathbb{C}H^{2}$. More precisely, we prove that a real hypersurface in 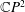$\mathbb{C}P^{2}$ or 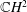$\mathbb{C}H^{2}$ with constant mean curvature is generalized 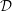${\mathcal{D}}$-Einstein with constant coefficient if and only if it is pseudo-Einstein. We prove that a real hypersurface in 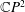$\mathbb{C}P^{2}$ with constant scalar curvature is generalized 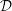${\mathcal{D}}$-Einstein with constant coefficient if and only if it is pseudo-Einstein.

Keywords

Real hypersurfacegeneralized 𝓓-Einsteinpseudo-Einsteinnonflat complex space form

MSC classification

Primary: 53B25: Local submanifolds
Secondary: 53D15: Almost contact and almost symplectic manifolds
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 4 , December 2020 , pp. 909 - 920
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the Key Scientific Research Program in Universities of Henan Province (No. 20A110023) and the Fostering Foundation of National Foundation in Henan Normal University (No. 2019PL22).

References

Cecil, T. E. and Ryan, P. J., Focal sets and real hypersurfaces in complex projective space. Trans. Amer. Math. Soc. 269(1982), 481–499. https://doi.org/10.2307/1998460Google Scholar
Cecil, T. E. and Ryan, P. J., Geometry of hypersurfaces. Springer Monographs in Mathematics, Springer, New York, 2015. https://doi.org/10.1007/978-1-4939-3246-7CrossRefGoogle Scholar
Ivey, T. A. and Ryan, P. J., Hopf hypersurfaces of small Hopf principal curvature in ℂH2. Geom. Dedicata 141(2009), 147–161. https://doi.org/10.1007/s10711-008-9349-7CrossRefGoogle Scholar
Ivey, T. A. and Ryan, P. J., The structure Jacobi operator for real hypersurfaces in ℂℙ2 and ℂH2. Results Math. 56(2009), 437–488. https://doi.org/10.1007/s00025-009-0380-2Google Scholar
Lim, D. H., Sohn, W. H., and Ahn, S. S., The property of real hypersurfaces in 2-dimensional complex space form with Ricci operator. Turkish J. Math. 38(2014), 920–923. https://doi.org/10.3906/mat-1310-19CrossRefGoogle Scholar
Lim, D. H., Sohn, W. H., and Song, H., A study of real hypersurfaces with Ricci operators in 2-dimensional complex space forms. Pacific J. Math. 266(2013), 305–311. https://doi.org/10.2140/pjm.2013.266.305CrossRefGoogle Scholar
Ki, U. H., Nakagawa, H., and Suh, Y. J., Real hypersurfaces with harmonic Weyl tensor of a complex space form. Hiroshima Math. J. 20(1990), 93–102. http://projecteuclid.org/euclid.hmj/1206454442CrossRefGoogle Scholar
Kim, H. S. and Ryan, P. J., A classification of pseudo-Einstein hypersurfaces in ℂP 2. Differ. Geom. Appl. 26(2008), 106–112. https://doi.org/10.1016/j.difgeo.2007.11.007CrossRefGoogle Scholar
Kon, M., Pseudo-Einstein real hypersurfaces in complex space forms. J. Differ. Geom. 14(1979), 339–354.CrossRefGoogle Scholar
Kon, M., A characterization of pseudo-Einstein real hypersurfaces of a complex space form. J. Appl. Anal. 19(2013), 167–179. https://doi.org/10.1515/jaa-2013-0010CrossRefGoogle Scholar
Kon, M., 3-dimensional real hypersurfaces and Ricci operator. Differ. Geom. Dyn. Syst. 16(2014), 189–202.Google Scholar
Kon, M., On pseudo-Einstein real hypersurfaces. Adv. Geom. https://doi.org/10.1515/advgeom-2019-0024Google Scholar
Maeda, Y., On real hypersurfaces of a complex projective space. J. Math. Soc. Japan 28(1976), 529–540. https://doi.org/10.2969/jmsj/02830529CrossRefGoogle Scholar
Montiel, S., Real hypersurfaces of a complex hyperbolic space. J. Math. Soc. Japan 37(1985), 515–535. https://doi.org/10.2969/jmsj/03730515CrossRefGoogle Scholar
Niebergall, R. and Ryan, P. J., Semi-parallel and semi-symmetric real hypersurfaces in complex space forms. Kyungpook Math. J. 38(1998), 227–234.Google Scholar
Niebergall, R. and Ryan, P. J., Real hypersurfaces in complex space forms. In: Tight and taut submanifolds (Berkeley, CA, 1994). Math. Sci. Res. Inst. Publ., 32, Cambridge University Press, Cambridge, 1997, pp. 233–305.Google Scholar
Ortega, M. and Pérez, J. D., D-Einstein real hypersurfaces of quaternionic space forms. Ann. Mat. Pura Appl. 178(2000), 33–44. https://doi.org/10.1007/BF02505886CrossRefGoogle Scholar
Panagiotidou, K., The structure Jacobi operator and the shape operator of real hypersurfaces in ℂP 2 and ℂH 2. Beitr. Algebra Geom. 55(2014), 545–556. https://doi.org/10.1007/s13366-013-0174-2CrossRefGoogle Scholar
Panagiotidou, K. and Xenos, P. J., Real hypersurfaces in ℂP 2 and ℂH 2 whose structure Jacobi operator is Lie 𝔻-parallel. Note Mat. 32(2012), 89–99. https://doi.org/10.1285/i15900932v32n2p89Google Scholar
Pérez, J. D., Some questions on the Ricci tensor of real hypersurfaces in a quaternion space form. In: Proceedings of the Fourth International Workshop on Differential Geometry (Taegu, 1999). Kyungpook Natl. Univ., Taegu, 2000, pp. 19–25.Google Scholar