No CrossRef data available.
Article contents
Homology supported in Lagrangian submanifolds in mirror quintic threefolds
Published online by Cambridge University Press: 11 September 2020
Abstract
In this note, we study homology classes in the mirror quintic Calabi–Yau threefold that can be realized by special Lagrangian submanifolds. We have used Picard–Lefschetz theory to establish the monodromy action and to study the orbit of Lagrangian vanishing cycles. For many prime numbers
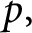 $p,$
we can compute the orbit modulo p. We conjecture that the orbit in homology with coefficients in
$p,$
we can compute the orbit modulo p. We conjecture that the orbit in homology with coefficients in
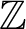 $\mathbb {Z}$
can be determined by these orbits with coefficients in
$\mathbb {Z}$
can be determined by these orbits with coefficients in
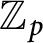 $\mathbb {Z}_p$
.
$\mathbb {Z}_p$
.
Keywords
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020



