Published online by Cambridge University Press: 06 May 2020
We prove that for  $0<p<+\infty $ and
$0<p<+\infty $ and 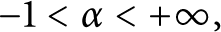 $-1<\alpha <+\infty ,$ a conformal map defined on the unit disk belongs to the weighted Bergman space
$-1<\alpha <+\infty ,$ a conformal map defined on the unit disk belongs to the weighted Bergman space 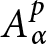 $A_{\alpha }^p$ if and only if a certain integral involving the hyperbolic distance converges.
$A_{\alpha }^p$ if and only if a certain integral involving the hyperbolic distance converges.
This research was co-financed by Greece and the European Union (European Social Fund-ESF) through the Operational Programme “Human Resources Development, Education and Lifelong Learning 2014–2020” in the context of the project “Angular derivatives and the hyperbolic metric” (MIS 5047551).