Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-10T13:55:26.823Z Has data issue: false hasContentIssue false
  • English
  • Français

Ideals of the Quantum Group Algebra, Arens Regularity and Weakly Compact Multipliers

Part of: Abstract harmonic analysis Selfadjoint operator algebras Topological algebras, normed rings and algebras, Banach algebras Infinite-dimensional manifolds

Published online by Cambridge University Press:  30 January 2020

Mehdi Nemati  and
Maryam Rajaei Rizi
Mehdi Nemati
Affiliation:
Department of Mathematical Sciences, Isfahan University of Technology, Isfahan 84156-83111, Iran School of Mathematics, Institute for Research in Fundamental Sciences (IPM), P.O. Box: 19395–5746, Tehran, Iran Email: m.nemati@iut.ac.ir
Maryam Rajaei Rizi
Affiliation:
Department of Mathematical Sciences, Isfahan University of Technology, Isfahan84156-83111, Iran Email: m.rajaierizi@math.iut.ac.ir
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 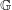$\mathbb{G}$ be a locally compact quantum group and let 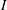$I$ be a closed ideal of 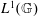$L^{1}(\mathbb{G})$ with 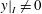$y|_{I}\neq 0$ for some 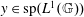$y\in \text{sp}(L^{1}(\mathbb{G}))$. In this paper, we give a characterization for compactness of 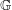$\mathbb{G}$ in terms of the existence of a weakly compact left or right multiplier 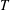$T$ on 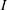$I$ with 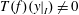$T(f)(y|_{I})\neq 0$ for some 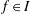$f\in I$. Using this, we prove that 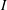$I$ is an ideal in its second dual if and only if 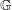$\mathbb{G}$ is compact. We also study Arens regularity of 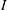$I$ whenever it has a bounded left approximate identity. Finally, we obtain some characterizations for amenability of 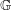$\mathbb{G}$ in terms of the existence of some 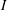$I$-module homomorphisms on 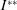$I^{\ast \ast }$ and on 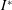$I^{\ast }$.

Keywords

amenabilityArens regularitylocally compact quantum group(weakly) compact multipliermodule homomorphism

MSC classification

Primary: 46H20: Structure, classification of topological algebras
Secondary: 46L89: Other “noncommutative” mathematics based on $C^*$-algebra theory 43A07: Means on groups, semigroups, etc.; amenable groups 43A22: Homomorphisms and multipliers of function spaces on groups, semigroups, etc. 58B32: Geometry of quantum groups
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 4 , December 2020 , pp. 825 - 836
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of the first author was supported in part by a grant from IPM (No. 98170411).

References

Amini, M., Kalantar, M., Medghalchi, A., Mollakhalili, A., and Neufang, M., Compact elements and operators of quantum groups. Glasg. Math. J. 59(2017), 445–462. https://doi.org/10.1017/S0017089516000276CrossRefGoogle Scholar
Bédos, E. and Tuset, L., Amenability and co-amenability for locally compact quantum groups. Internat. J. Math. 14(2003), 865–884. https://doi.org/10.1142/S0129167X03002046CrossRefGoogle Scholar
Daws, M. and Lepham, H., Isometries between quantum convolution algebras. Q. J. Math. 64(2013), 373–396. https://doi.org/10.1093/qmath/has008CrossRefGoogle Scholar
Duncan, J. and Hosseiniun, S. A. R., The second dual of a Banach algebra. Proc. Roy. Soc. Edinburgh Sect. A 84(1979), 309–325. https://doi.org/10.1017/S0308210500017170CrossRefGoogle Scholar
Forrest, B., Arens regularity and discrete groups. Pacific J. Math. 151(1991), 217–227.CrossRefGoogle Scholar
Ghahramani, F. and Lau, A. T.-M., Multipliers and ideals in second conjugate algebras related to locally compact groups. J. Funct. Anal. 132(1995), 170–191. https://doi.org/10.1006/jfan.1995.1104CrossRefGoogle Scholar
Ghahramani, F. and Lau, A. T.-M., Multipliers and modulus on Banach algebras related to locally compact groups. J. Funct. Anal. 150(1997), 478–497. https://doi.org/10.1006/jfan.1997.3133CrossRefGoogle Scholar
Ghanei, M., Nasr-Isfahani, R., and Nemati, M., A homological property and Arens regularity of locally compact quantum groups. Canad. Math. Bull. 60(2017), no. 1, 122–130. https://doi.org/10.4153/CMB-2016-052-xCrossRefGoogle Scholar
Hu, Z., Neufang, M., and Ruan, Z.-J., On topological center problems and SIN quantum groups. J. Funct. Anal. 257(2009), 610–640. https://doi.org/10.1016/j.jfa.2009.02.004CrossRefGoogle Scholar
Kalantar, M. and Neufang, M., From quantum groups to groups. Canadian J. Math. 65(2013), 1073–1094. https://doi.org/10.4153/CJM-2012-047-xCrossRefGoogle Scholar
Kaniuth, E., Lau, A. T.-M., and Pym, J., On 𝜑-amenability of Banach algebras. Math. Proc. Cambridge Philos. Soc. 144(2008), 85–96. https://doi.org/10.1017/S0305004107000874CrossRefGoogle Scholar
Kaniuth, E., Lau, A. T.-M., and Pym, J., On character amenability of Banach algebras. J. Math. Anal. Appl. 344(2008), 942–955. https://doi.org/10.1016/j.jmaa.2008.03.037CrossRefGoogle Scholar
Kustermans, J. and Vaes, S., Locally compact quantum groups. Ann. Sci. École Norm. Sup. 33(2000), 837–934. https://doi.org/10.1016/S0012-9593(00)01055-7CrossRefGoogle Scholar
Kustermans, J. and Vaes, S., Locally compact quantum groups in the von Neumann algebraic setting. Math. Scand. 92(2003), 68–92. https://doi.org/10.7146/math.scand.a-14394CrossRefGoogle Scholar
Lau, A. T.-M., Uniformly continuous functionals on the Fourier algebra of any locally compact group. Trans. Am. Math. Soc. 251(1979), 39–59. https://doi.org/10.2307/1998682CrossRefGoogle Scholar
Losert, V., Weakly compact multipliers on group algebras. J. Funct. Anal. 213(2004), 466–472. https://doi.org/10.1016/j.jfa.2003.10.012CrossRefGoogle Scholar
Ruan, Z.-J., Amenability of Hopf von Neumann algebras and Kac algebras. J. Funct. Anal. 139(1996), 466–499. https://doi.org/10.1006/jfan.1996.0093CrossRefGoogle Scholar
Runde, V., Characterizations of compact and discrete quantum groups through second duals. J. Operator Theory 60(2008), 415–428.Google Scholar
Sakai, S., Weakly compact operators on operator algebras. Pac. J. Math. 14(1964), 659–664.CrossRefGoogle Scholar
Ulger, A., Arens regularity sometimes implies RNP. Pacific J. Math. 143(1990), 377–399.CrossRefGoogle Scholar