No CrossRef data available.
Article contents
New Facts about the Vanishing Off Subgroup 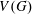 $V(G)$
$V(G)$
Published online by Cambridge University Press: 23 August 2019
Abstract
In this manuscript, we generalize Lewis’s result about a central series associated with the vanishing off subgroup. We write 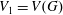 $V_{1}=V(G)$ for the vanishing off subgroup of
$V_{1}=V(G)$ for the vanishing off subgroup of 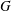 $G$, and
$G$, and 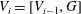 $V_{i}=[V_{i-1},G]$ for the terms in this central series. Lewis proved that there exists a positive integer
$V_{i}=[V_{i-1},G]$ for the terms in this central series. Lewis proved that there exists a positive integer  $n$ such that if
$n$ such that if 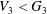 $V_{3}<G_{3}$, then
$V_{3}<G_{3}$, then 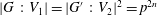 $|G\,:\,V_{1}|=|G^{\prime }\,:\,V_{2}|^{2}=p^{2n}$. Let
$|G\,:\,V_{1}|=|G^{\prime }\,:\,V_{2}|^{2}=p^{2n}$. Let 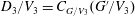 $D_{3}/V_{3}=C_{G/V_{3}}(G^{\prime }/V_{3})$. He also showed that if
$D_{3}/V_{3}=C_{G/V_{3}}(G^{\prime }/V_{3})$. He also showed that if 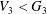 $V_{3}<G_{3}$, then either
$V_{3}<G_{3}$, then either 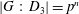 $|G\,:\,D_{3}|=p^{n}$ or
$|G\,:\,D_{3}|=p^{n}$ or 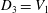 $D_{3}=V_{1}$. We show that if
$D_{3}=V_{1}$. We show that if 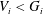 $V_{i}<G_{i}$ for
$V_{i}<G_{i}$ for 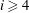 $i\geqslant 4$, where
$i\geqslant 4$, where 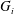 $G_{i}$ is the
$G_{i}$ is the  $i$-th term in the lower central series of
$i$-th term in the lower central series of 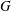 $G$, then
$G$, then 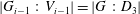 $|G_{i-1}\,:\,V_{i-1}|=|G\,:\,D_{3}|$.
$|G_{i-1}\,:\,V_{i-1}|=|G\,:\,D_{3}|$.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019


