Article contents
A Note on Chirally Cosmetic Surgery on Cable Knots
Published online by Cambridge University Press: 29 April 2020
Abstract
We show that a 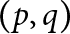 $(p,q)$-cable of a non-trivial knot K does not admit chirally cosmetic surgeries for
$(p,q)$-cable of a non-trivial knot K does not admit chirally cosmetic surgeries for 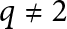 $q\neq 2$, or
$q\neq 2$, or 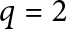 $q=2$ with additional assumptions. In particular, we show that a
$q=2$ with additional assumptions. In particular, we show that a  $(p,q)$-cable of a non-trivial knot K does not admit chirally cosmetic surgeries as long as the set of JSJ pieces of the knot exterior does not contain the
$(p,q)$-cable of a non-trivial knot K does not admit chirally cosmetic surgeries as long as the set of JSJ pieces of the knot exterior does not contain the 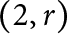 $(2,r)$-torus exterior for any r. We also show that an iterated torus knot other than the
$(2,r)$-torus exterior for any r. We also show that an iterated torus knot other than the 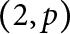 $(2,p)$-torus knot does not admit chirally cosmetic surgery.
$(2,p)$-torus knot does not admit chirally cosmetic surgery.
Keywords
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
Footnotes
The author has been partially supported by JSPS KAKENHI Grant Number 19K03490, 16H02145.
References
- 1
- Cited by



