No CrossRef data available.
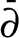 $ \bar {\partial } $-Riemann–Hilbert method
$ \bar {\partial } $-Riemann–Hilbert methodPublished online by Cambridge University Press: 24 February 2022
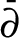 $\bar {\partial } $
-extension of the matrix Riemann–Hilbert method is used to study asymptotics of the polynomials
$\bar {\partial } $
-extension of the matrix Riemann–Hilbert method is used to study asymptotics of the polynomials
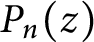 $ P_n(z) $
satisfying orthogonality relations
$ P_n(z) $
satisfying orthogonality relations
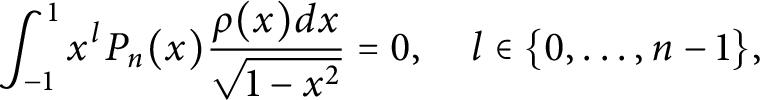 $$ \begin{align*} \int_{-1}^1 x^lP_n(x)\frac{\rho(x)dx}{\sqrt{1-x^2}}=0, \quad l\in\{0,\ldots,n-1\}, \end{align*} $$
$$ \begin{align*} \int_{-1}^1 x^lP_n(x)\frac{\rho(x)dx}{\sqrt{1-x^2}}=0, \quad l\in\{0,\ldots,n-1\}, \end{align*} $$
where
 $ \rho (x) $
is a positive
$ \rho (x) $
is a positive
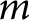 $ m $
times continuously differentiable function on
$ m $
times continuously differentiable function on
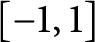 $ [-1,1] $
,
$ [-1,1] $
,
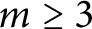 $ m\geq 3 $
.
$ m\geq 3 $
.
The research was supported by a grant from the Simons Foundation, CGM-706591.