No CrossRef data available.
Article contents
A Vanishing Theorem for the Twisted Normal Bundle of Curves in 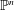 $\mathbb{P}^{n}$,
$\mathbb{P}^{n}$, 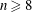 $n\geqslant 8$
$n\geqslant 8$
Published online by Cambridge University Press: 30 August 2019
Abstract
We prove the existence of a smooth and non-degenerate curve 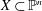 $X\subset \mathbb{P}^{n}$,
$X\subset \mathbb{P}^{n}$, 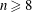 $n\geqslant 8$, with
$n\geqslant 8$, with 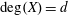 $\deg (X)=d$,
$\deg (X)=d$, 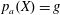 $p_{a}(X)=g$,
$p_{a}(X)=g$, 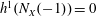 $h^{1}(N_{X}(-1))=0$, and general moduli for all
$h^{1}(N_{X}(-1))=0$, and general moduli for all 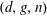 $(d,g,n)$ such that
$(d,g,n)$ such that 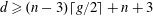 $d\geqslant (n-3)\lceil g/2\rceil +n+3$. It was proved by C. Walter that, for
$d\geqslant (n-3)\lceil g/2\rceil +n+3$. It was proved by C. Walter that, for 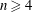 $n\geqslant 4$, the inequality
$n\geqslant 4$, the inequality 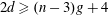 $2d\geqslant (n-3)g+4$ is a necessary condition for the existence of a curve with
$2d\geqslant (n-3)g+4$ is a necessary condition for the existence of a curve with 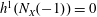 $h^{1}(N_{X}(-1))=0$.
$h^{1}(N_{X}(-1))=0$.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2019
Footnotes
The author was partially supported by MIUR and GNSAGA of INdAM (Italy).


