Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T17:07:44.192Z Has data issue: false hasContentIssue false
  • English
  • Français

Affine Actions of Uq(sl(2)) on Polynomial Rings

Published online by Cambridge University Press:  20 November 2018

Jeffrey Bergen
Jeffrey Bergen*
Affiliation:
Department of Mathematics, DePaul University, 2320 N. Kenmore Avenue, Chicago, Illinois 60614, USA. e-mail: jbergen@depaul.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We classify the affine actions of 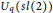${{U}_{q}}\left( sl\left( 2 \right) \right)$ on commutative polynomial rings in 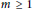$m\,\ge \,1$ variables. We show that, up to scalar multiplication, there are two possible actions. In addition, for each action, the subring of invariants is a polynomial ring in either $m$ or 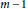$m\,-\,1$ variables, depending upon whether $q$ is or is not a root of 1.

Keywords

16T2017B3720G42skew derivationquantum groupinvariants
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 2 , 01 June 2015 , pp. 233 - 240
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Brown, K. A. and Goodearl, K. R., Lectures on algebraic quantum groups. Advanced Courses in Mathematics. CRM Barcelona, Birkhâuser Verlag, Basel, 2002.Google Scholar
[2] Hu, N., Realization of quantized algebra of type A as Hopf algebra over quantum space. Comm. Algebra 29 (2001), no. 2, 529–539. http://dx.doi.org/10.1081/ACB-100001522 Google Scholar
[3] Hu, N., Montgomery, S. and Smith, S. P., Skew derivations and Uq(sl(2)). Israel J. Math. 72 (1990), no. 1–2, 158–166. http://dx.doi.org/10.1007/BF02764618 Google Scholar