Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cockayne, E. J.
1972.
Colour Classes for r-Graphs.
Canadian Mathematical Bulletin,
Vol. 15,
Issue. 3,
p.
349.
Parsons, T.D.
1973.
The Ramsey numbers r(Pm, Kn).
Discrete Mathematics,
Vol. 6,
Issue. 2,
p.
159.
Burr, Stefan A.
1974.
Graphs and Combinatorics.
Vol. 406,
Issue. ,
p.
52.
Harary, Frank
1974.
Graphs and Combinatorics.
Vol. 406,
Issue. ,
p.
10.
Parsons, T. D.
1975.
Ramsey graphs and block designs. I.
Transactions of the American Mathematical Society,
Vol. 209,
Issue. 0,
p.
33.
Cockayne, E. J.
and
Lorimer, P. J.
1975.
The Ramsey number for stripes.
Journal of the Australian Mathematical Society,
Vol. 19,
Issue. 2,
p.
252.
Cockayne, E. J.
and
Lorimer, P. J.
1975.
On Ramsey Graph Numbers for Stars and Stripes.
Canadian Mathematical Bulletin,
Vol. 18,
Issue. 1,
p.
31.
Burr, S. A.
Erdős, P.
and
Spencer, J. H.
1975.
Ramsey theorems for multiple copies of graphs.
Transactions of the American Mathematical Society,
Vol. 209,
Issue. 0,
p.
87.
Parsons, T.D
1976.
Ramsey graphs and block designs.
Journal of Combinatorial Theory, Series A,
Vol. 20,
Issue. 1,
p.
12.
Lorimer, P.J
and
Mullins, P.R
1977.
Ramsey numbers for quadrangles and triangles.
Journal of Combinatorial Theory, Series B,
Vol. 23,
Issue. 2-3,
p.
262.

 such that for each
such that for each 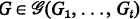 if the edges of
if the edges of 