No CrossRef data available.
Published online by Cambridge University Press: 07 December 2020
Let  $\Omega $
be homogeneous of degree zero and have mean value zero on the unit sphere
$\Omega $
be homogeneous of degree zero and have mean value zero on the unit sphere 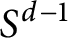 ${S}^{d-1}$
,
${S}^{d-1}$
, 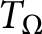 $T_{\Omega }$
be the convolution singular integral operator with kernel
$T_{\Omega }$
be the convolution singular integral operator with kernel 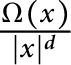 $\frac {\Omega (x)}{|x|^d}$
. In this paper, we prove that if
$\frac {\Omega (x)}{|x|^d}$
. In this paper, we prove that if 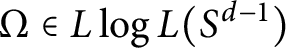 $\Omega \in L\log L(S^{d-1})$
, and U is an operator which is bounded on
$\Omega \in L\log L(S^{d-1})$
, and U is an operator which is bounded on 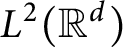 $L^2(\mathbb {R}^d)$
and satisfies the weak type endpoint estimate of
$L^2(\mathbb {R}^d)$
and satisfies the weak type endpoint estimate of 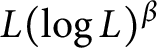 $L(\log L)^{\beta }$
type, then the composition operator
$L(\log L)^{\beta }$
type, then the composition operator 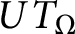 $UT_{\Omega }$
satisfies a weak type endpoint estimate of
$UT_{\Omega }$
satisfies a weak type endpoint estimate of 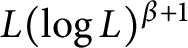 $L(\log L)^{\beta +1}$
type.
$L(\log L)^{\beta +1}$
type.
The research of X.T was supported by the NNSF of China under grant #11771399, and the research of G.H. (corresponding author) was supported by the NNSF of China under grant #11871108.